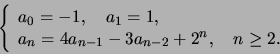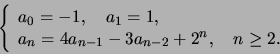Next: About this document ...
Up: fe_010328
Previous: fe_010328
- A mid-size university department has six working groups
developing the department's Teaching Quality Initiatives.
Five professors (A,...,E) participate in these groups,
according to the following scheme:
| 1: A, B, C |
4: B, C, D |
| 2: A, C, D |
5: B, E |
| 3: A, E |
6: C, D, E |
Each working group meeting requires a full day, and
obviously no two groups with common members can be
scheduled for the same day. Design a graph-theoretic
model of the situation, and determine on this basis how
many days are needed for each group to hold at least one meeting.
- The student association of the abovementioned department
selects ten representatives to work on the Teaching Quality
Initiatives, so that each of these ten persons participates
in the workings of exactly one of the groups 1-6. Compute
the number of ways the groups' student representations can
be arranged, under the conditions that each group must
have at least one student member, but at most as many as there
are professor members in that group.
(For the purposes of this problem, students are considered
to be identical, so that it is only significant how many
student representatives there are in each working group.)
- Our example department has been awarded for its development work
a Quality Diplom by the Rector, and each of the professors
A,...,E may now hold the Diplom on their bookshelf one
week at a time. Design for the Diplom a 10-week rotation
schedule, during which each pair of professors who had worked
together in some of the groups 1-6 exhanges the diplom
exactly once. (The direction of the exchange, i.e. who
forwards the Diplom to whom, does not matter.)
- Find a closed form solution for the recurrence equation:
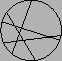
- A round pizza is cut into pieces by
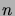 knife cuts,
so that any two cuts meet pairwise,
but no three at the same point (cf. Figure 1).
Prove that the cuts divide the pizza into
knife cuts,
so that any two cuts meet pairwise,
but no three at the same point (cf. Figure 1).
Prove that the cuts divide the pizza into
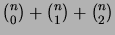 pieces.
(Hint: One way to solve the problem is to
view the pizza as a plane graph.)
pieces.
(Hint: One way to solve the problem is to
view the pizza as a plane graph.)
Figure 1:
A sliced pizza
 |
Grading: Each problem 12 points, total 60 points.



Next: About this document ...
Up: fe_010328
Previous: fe_010328
Pekka Orponen
2001-03-28