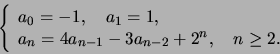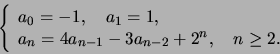MAT282 Johdatus diskreettiin matematiikkaan (3 ov)
Loppukoe ke 28.3.2001 klo 8-12

1. Erään keskikokoisen yliopistollisen laitoksen opetuksenkehittämishankkeita valmistelee kuusi työryhmää, joiden toimintaan osallistuu laitokselta viisi professoria A,...,E. Työryhmien kokoonpanot ovat seuraavat:

   1: A, B, C	4: B, C, D
   2: A, C, D	5: B, E
   3: A, E	6: C, D, E

   Kukin työryhmäkokous vaatii kokonaisen päivän, eikä kaksi ryhmää joissa on yhteisiä jäseniä tietenkään voi kokoontua samaan aikaan. Laadi tilanteesta verkkoteoreettinen malli ja päättele tämän nojalla, montako kokouspäivää tarvitaan, jotta kaikki työryhmät ehtivät kokoontua vähintään yhden kerran.

2. Tehtävän 1 laitoksen opiskelijajärjestö valitsee keskuudestaan kehittämistyöryhmiin kymmenen edustajaa, joista kukin osallistuu täsmälleen yhden ryhmistä 1-6 työskentelyyn. Monellako tavalla ryhmien opiskelijaedustukset voidaan muodostaa, kun vaatimuksena on, että kuhunkin ryhmään tulee vähintään yksi opiskelijajäsen, ja enintään yhtä monta kuin ryhmässä on professorijäseniä? (Tarkastellaan opiskelijoita tässä yksinkertaisuuden vuoksi identtisinä, niin että merkitystä on vain sillä, montako opiskelijajäsentä kuhunkin ryhmään tulee.)

3. Tehtävän 1 laitos sai palkinnoksi kehittämistyöstään rehtorin kunniakirjan, jota kukin professoreista A,...,E saa pitää hyllyssään viikon kerrallaan. Suunnittele kunniakirjalle kiertojärjestys, jossa 10 viikon kuluessa kukin jossain työryhmässä yhdessä työskennellyt professoripari vaihtaa kirjan yhden kerran keskenään. (Vaihdon suunnalla, so. sillä kumpi antaa kirjan toiselle, ei ole merkitystä.)

4. Ratkaise rekursioyhtälö:
   
   $$\left\{\begin{array}{l} a_0 = -1, \quad a_1 = 1,\\ a_n = 4a_{n-1}-3a_{n-2}+2^n, \quad n \geq 2. \end{array}\right.$$
   
   

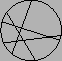
5. Pyöreään pizzaan tehdään kuvan 1 esittämällä tavall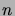a $n$ koko pizzan ylittävää viiltoa, jotka kaikki leikkaavat toisensa pareittain, mutta mitkään kolme eivät leikkaa samassa pisteessä. Osoita, että leikkaukset jakavat pizzan ${{n}\choose{0}} + {{n}\choose{1}} + {{n}\choose{2}}$ palaan. (Vihje: Yksi tapa ratkaista tehtävä on tarkastella pizzaa tasoverkkona.)

   Kuva 1: Leikattu pizza

   

Pisteytys: Kukin tehtävä 12 pistettä, yhteensä 60 pistettä.