


Next: About this document ...
Up: fe_010124
Previous: fe_010124
- Draw a Hasse diagram of the partially ordered set
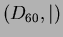 , formed by the integer divisors of number 60,
, formed by the integer divisors of number 60,
 ,
ordered according to the integer divisibility relation:
,
ordered according to the integer divisibility relation:
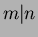 if
if 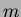 is a factor of
is a factor of 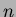 .
.
- A final exam contains 5 problems whose grading should
be allocated among 3 graders (A, B, C) so that each
grader is responsible for at least one problem.
In how many ways can the partitioning of the problems
be done, when:
- The numbering of the problems is not significant,
so that the only thing to consider is how many problems
are allocated to each of A, B, C.
- The numbering of the problems is important,
but it does not matter who is responsible for
which set of problems.
- Both the numbering of the problems and the
graders' identities are taken into consideration.
- A final exam contains 5 problems, each of which is
worth 0-12 points. In how many ways can one reach an
exact total of 30 points in the exam, under the condition
that one must get at least 1 point from each problem?
(The numbering of the problems is significant, so that
e.g. the result 1-2-3-12-12 is considered to be different
from 12-12-3-2-1.) -- If you don't have a calculator
with you, providing the appropriate binomial coefficient
formula suffices.
- Prove that a connected graph
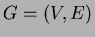 ,
, 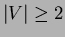 ,
is bipartite (i.e.
,
is bipartite (i.e. 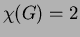 ), if and only if
), if and only if
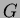 doesn't contain odd cycles, i.e. if no subgraph
of
doesn't contain odd cycles, i.e. if no subgraph
of 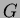 is of the form
is of the form 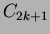 ,
, 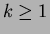 .
.
- A derangement on
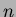 elements
is a permutation
elements
is a permutation
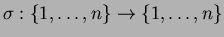 ,
such that
,
such that
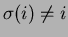 for all
for all 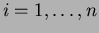 .
Prove, using the principle of inclusion and exclusion,
that the number of
.
Prove, using the principle of inclusion and exclusion,
that the number of 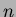 -element derangements equals
-element derangements equals
(Additional information, unrelated to solving
the problem: The formula shows that the number of
derangements quickly approaches 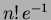 as
as
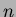 grows. Thus, a randomly chosen permutation on
grows. Thus, a randomly chosen permutation on
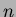 elements is a derangement approximately with
probability
elements is a derangement approximately with
probability 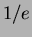 .)
.)
Grading: Each problem 12 points, total 60 points.



Next: About this document ...
Up: fe_010124
Previous: fe_010124
Pekka Orponen
2001-01-24