


Next: Tästä dokumentista ...
Up: lk_010124
Previous: lk_010124
- Piirrä Hasse-kaavio osittainjärjestetystä joukosta
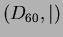 , missä perusjoukkona ovat luvun 60
kokonaislukutekijät
, missä perusjoukkona ovat luvun 60
kokonaislukutekijät
 ,
ja järjestysrelaationa kokonaislukujen jaollisuusrelaatio:
,
ja järjestysrelaationa kokonaislukujen jaollisuusrelaatio:
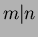 , jos luku
, jos luku 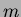 on luvun
on luvun 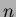 tekijä.
tekijä.
- Tentissä on 5 tehtävää, joiden tarkastaminen halutaan
jakaa 3 tarkastajan (A, B, C) kesken niin, että
jokainen saa tarkastaakseen vähintään yhden tehtävän.
Monellako tavalla ositus voidaan tehdä, kun:
- Tehtävien numeroinnilla ei ole väliä, so. ollaan kiinnostuneita vain siitä, montako tehtävää
kukin tarkastajista A, B, C saa lukeakseen.
- Tehtävien numerointi on tärkeä, mutta sen
sijaan sillä kuka tarkastaa minkä tehtäväjoukon
ei ole merkitystä.
- Sekä tehtävien numerointi että tarkastajien
henkilöllisyys otetaan huomioon.
- Tentissä on 5 tehtävää, joista kustakin voi saada 0-12
pistettä. Monellako tavalla tentistä voi saada tulokseksi
tasan 30 pistettä niin, että jokaisesta tehtävästä
saa vähintään 1 pisteen? (Tehtävien numerointi otetaan
huomioon, so. esimerkiksi pistejakauma 1-2-3-12-12
on eri kuin pistejakauma 12-12-3-2-1.) -- Jos sinulla
ei ole laskinta, ratkaisuksi riittää asianmukainen
binomikerroinlauseke.
- Todista, että yhtenäinen verkko
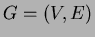 ,
, 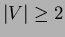 ,
on kaksijakoinen (so.
,
on kaksijakoinen (so. 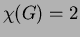 ), jos ja vain jos
), jos ja vain jos
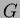 ei sisällä parittomia syklejä, so. jos mikään
ei sisällä parittomia syklejä, so. jos mikään 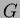 :n
aliverkko ei ole muotoa
:n
aliverkko ei ole muotoa 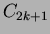 ,
, 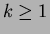 .
.
- Tarkastellaan
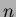 alkion sekoituksia
(engl. derangements), so. permutaatioita
alkion sekoituksia
(engl. derangements), so. permutaatioita
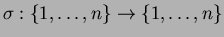 ,
joilla
,
joilla
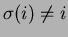 kaikilla
kaikilla 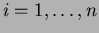 .
Osoita seulayhtälöä käyttäen, että
.
Osoita seulayhtälöä käyttäen, että 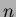 alkion
sekoituksia on kaikkiaan
alkion
sekoituksia on kaikkiaan
kappaletta. (Lisätieto, ei liity tehtävän
ratkaisemiseen: Kaava osoittaa, että sekoitusten määrä
lähestyy 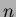 :n kasvaessa nopeasti arvoa
:n kasvaessa nopeasti arvoa 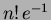 .
Siten on satunnaisesti valittu
.
Siten on satunnaisesti valittu 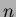 alkion permutaatio
sekoitus likimäärin todennäköisyydellä
alkion permutaatio
sekoitus likimäärin todennäköisyydellä 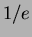 .)
.)
Pisteytys: Kukin tehtävä 12 pistettä, yhteensä 60 pistettä.



Next: Tästä dokumentista ...
Up: lk_010124
Previous: lk_010124
Pekka Orponen
2001-01-24