Next: Tästä dokumentista ...
Up: vk_001129
Previous: vk_001129
- Anna esimerkit yhtenäisistä verkoista, joissa:
- ei ole Eulerin kierrosta eikä Hamiltonin kehää;
- on Eulerin kierros mutta ei Hamiltonin kehää;
- on Hamiltonin kehä mutta ei Eulerin kierrosta;
- on sekä Eulerin kierros että Hamiltonin kehä.
- Merkitään verkon
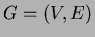 solmujen keskimääräistä astetta
solmujen keskimääräistä astetta
Osoita, että kaikilla tasoverkoilla 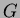 on
on
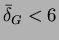 , ja että puiden
, ja että puiden 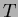 keskimääräinen
aste lähestyy raja-arvoa
keskimääräinen
aste lähestyy raja-arvoa
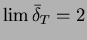 ,
kun solmujen lukumäärä kasvaa.
,
kun solmujen lukumäärä kasvaa.
- Hyperkuutioverkon
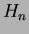 solmuina ovat kaikki
solmuina ovat kaikki 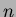 -bittiset
binäärijonot
-bittiset
binäärijonot
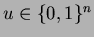 , ja solmujen
, ja solmujen 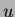 ja
ja 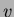 välillä
on kaari, jos ja vain jos niitä vastaavat binäärijonot eroavat
toisistaan tasan yhdessä kohden. Määritä hyperkuutioverkon
välillä
on kaari, jos ja vain jos niitä vastaavat binäärijonot eroavat
toisistaan tasan yhdessä kohden. Määritä hyperkuutioverkon
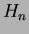 väriluku
väriluku 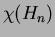 . (Perusteltu vastaus.)
. (Perusteltu vastaus.)
- Suunnittele jokin kuusibittinen, yhden virheen korjaava
lineaarinen koodi, jossa on 8 koodisanaa. Esitä koodisi
tarkistusmatriisi ja luettele sen mukaiset koodisanat.
Esitä, miten jokin yhden bittivirheen sisältävä jono
korjattaisiin suunnittelemaasi tarkistusmatriisia käyttäen.
Pisteytys: tehtävät 1 ja 2 á 8 pistettä, tehtävät 3 ja 4
á 7 pistettä, yhteensä 30 pistettä.



Next: Tästä dokumentista ...
Up: vk_001129
Previous: vk_001129
Pekka Orponen
2000-12-09