


Next: Tästä dokumentista ...
Up: lk_001115
Previous: lk_001115
- Olkoot
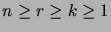 kokonaislukuja.
Todista oikeiksi seuraavat binomikerroinyhtälöt:
kokonaislukuja.
Todista oikeiksi seuraavat binomikerroinyhtälöt:
Anna jälkimmäiselle yhtälölle myös kombinatorinen tulkinta.
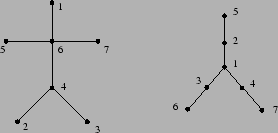
- Muodosta seuraavien puiden Prüfer-koodit:
Minkä 8-solmuisen puun Prüfer-koodi on (2,7,1,8,2,8)?
- Osoita, että jokaisen vähintään kaksisolmuisen
puun
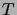 väriluku on
väriluku on 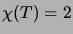 .
.
- Osoita, että jos puussa on solmu, jonka
asteluku on
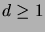 , niin siinä on myös
vähintään
, niin siinä on myös
vähintään 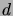 lehteä.
lehteä.
- Piirrä verkko, jonka solmuina ovat nelialkioisen
perusjoukon
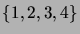 kaikki kaksialkioiset
osajoukot, ja solmujen
kaikki kaksialkioiset
osajoukot, ja solmujen 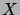 ja
ja 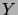 ,
, 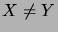 ,
välillä on kaari, jos ja vain jos
,
välillä on kaari, jos ja vain jos
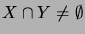 .
Osoita, että näin saatu verkko on planaarinen.
.
Osoita, että näin saatu verkko on planaarinen.
- Osoita, että vastaavalla tavalla viisialkioisen
perusjoukon
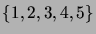 kaksialkioisista osajoukoista
muodostettu verkko ei ole planaarinen.
kaksialkioisista osajoukoista
muodostettu verkko ei ole planaarinen.
- A:n tasavallan presidentinvaalien ääntenlaskussa on
syntynyt kiperä tilanne: 370 Aku Ankalle (joka ei ollut
ehdokkaana) annettua ääntä pitäisi jakaa ehdokkaiden
B, G ja N kesken niin, että ehdokas B saa vähintään 200
ääntä, ehdokas G 100-199 ääntä ja ehdokas N enintään 10
ääntä. Monellako tavalla toivottu akuankkaäänten ositus
voidaan suorittaa?
- Tarkastellaan nelimerkkisen aakkoston
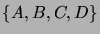 merkkijonoja. Merkitään
merkkijonoja. Merkitään 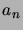 :llä sellaisten
:llä sellaisten
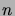 -merkkisten jonojen määrää, jotka
sisältävät parittoman määrän
-merkkisten jonojen määrää, jotka
sisältävät parittoman määrän 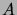 -merkkejä.
(Siten
-merkkejä.
(Siten 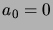 ,
, 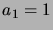 ,
, 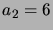 jne.) Osoita,
että lukuja
jne.) Osoita,
että lukuja 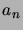 yhdistää rekursioyhtälö
yhdistää rekursioyhtälö
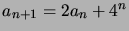 , ja ratkaise tästä
luvut
, ja ratkaise tästä
luvut 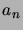 suljetussa muodossa.
(Vihje: Osita
suljetussa muodossa.
(Vihje: Osita 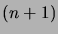 :n mittaiset merkkijonot
sen mukaan, alkavatko ne
:n mittaiset merkkijonot
sen mukaan, alkavatko ne 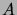 :lla vai jollain muulla
merkillä.)
:lla vai jollain muulla
merkillä.)
Pisteytys: Kukin tehtävä 12 pistettä, yhteensä 60 pistettä.



Next: Tästä dokumentista ...
Up: lk_001115
Previous: lk_001115
Pekka Orponen
2000-11-15
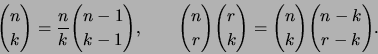
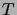 väriluku on
väriluku on 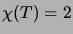 .
.
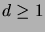 , niin siinä on myös
vähintään
, niin siinä on myös
vähintään 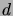 lehteä.
lehteä.
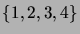 kaikki kaksialkioiset
osajoukot, ja solmujen
kaikki kaksialkioiset
osajoukot, ja solmujen 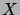 ja
ja 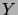 ,
, 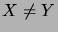 ,
välillä on kaari, jos ja vain jos
,
välillä on kaari, jos ja vain jos
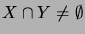 .
Osoita, että näin saatu verkko on planaarinen.
.
Osoita, että näin saatu verkko on planaarinen.
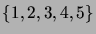 kaksialkioisista osajoukoista
muodostettu verkko ei ole planaarinen.
kaksialkioisista osajoukoista
muodostettu verkko ei ole planaarinen.