


Next: About this document
Up: No Title
Previous: No Title
-
-
Monenko positiivisten kokonaislukujen muodostaman kolmikon
(k,l,m) kautta kulkee avaruuden
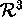 taso
x + y + z = r,
taso
x + y + z = r, 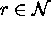 ?
? -
Monellako tavalla voidaan viiden tentin osallistujat sijoittaa
kolmeen saliin, kun vaaditaan että kaikki tiettyyn tenttiin
osallistuvat sijoittuvat samaan saliin, ja mikään sali ei
jää tyhjäksi?
-
Erääseen autourheilusarjaan osallistuu neljä merkkitallia.
Monellako tavalla voidaan näiden kesken järjestää kymmenen
auton osakilpailu, kun vaaditaan että kustakin tallista
on oltava mukana vähintään yksi ja enintään kolme autoa?
(Saman tallin autot ja kuljettajat ovat keskenään identtisiä;
ainoastaan autojen lukumäärällä on merkitystä.)
-
Tasoon piirretään n ei-yhdensuuntaista suoraa niin, että
mitkään kolme niistä eivät leikkaa samassa pisteessä.
(So. jokainen ``uusi'' suora leikkaa kaikki ``vanhat''
suorat, kunkin eri pisteessä.) Merkitään
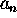 :llä näin
muodostuvien erillisten tasoalueiden määrää: siis
:llä näin
muodostuvien erillisten tasoalueiden määrää: siis
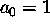 ,
, 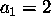 ,
, 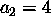 ,
, 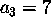 jne.
Muodosta perusteltu rekursioyhtälö lukujonolle
jne.
Muodosta perusteltu rekursioyhtälö lukujonolle 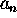 ja
ratkaise se.
ja
ratkaise se. -
Montako solmua ja montako kaarta on täydellisessä
kaksijakoisessa verkossa
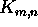 ? Millä ehdoilla
verkko
? Millä ehdoilla
verkko 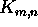 on planaarinen? (Perusteltu vastaus.)
on planaarinen? (Perusteltu vastaus.) -
-
Olkoon G mielivaltainen yhtenäinen (suuntaamaton) verkko. Osoita,
että jos G ei ole valmiiksi parillisasteinen (so. kaikkien
solmujen asteluku ei ole parillinen), niin G voidaan
täydentää sellaiseksi lisäämällä yksi uusi solmu u
ja tarvittavat kaaret solmun u ja verkon G ``vanhojen''
solmujen välille.
-
Käyttäen hyväksi edellisen kohdan tulosta todista oikeaksi
seuraava väite: minkä tahansa yhtenäisen verkon G kaaret
voidaan suunnistaa niin, että syntyvässä suhteikossa (suunnatussa
verkossa)
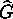 on kunkin solmun tulo- ja lähtöasteiden
(so. solmua ``kohden'' ja siitä ``poispäin'' suunnattujen
kaarten määrän) erotus enintään 1.
on kunkin solmun tulo- ja lähtöasteiden
(so. solmua ``kohden'' ja siitä ``poispäin'' suunnattujen
kaarten määrän) erotus enintään 1.
Pisteytys: Kukin tehtävä 12 pistettä, yhteensä 60 pistettä.
Pekka Orponen
Wed Mar 29 14:41:36 EET DST 2000
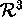 taso
x + y + z = r,
taso
x + y + z = r, 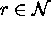 ?
?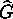 on kunkin solmun tulo- ja lähtöasteiden
(so. solmua ``kohden'' ja siitä ``poispäin'' suunnattujen
kaarten määrän) erotus enintään 1.
on kunkin solmun tulo- ja lähtöasteiden
(so. solmua ``kohden'' ja siitä ``poispäin'' suunnattujen
kaarten määrän) erotus enintään 1.