![]()
(Vihje: Tarkastele lukujen ![]() sijaan niiden 2-kantaisia
logaritmeja
sijaan niiden 2-kantaisia
logaritmeja ![]() .)
.)
- Piirrä verkko
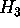 .
. - Millä n:n arvoilla verkko
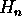 sisältää Eulerin kierroksen?
sisältää Eulerin kierroksen? - Mikä on verkon
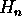 väriluku? (Perusteltu vastaus.)
väriluku? (Perusteltu vastaus.) - Osoita, että jos
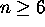 , niin verkko
, niin verkko 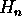 ei ole planaarinen. (Bonustehtävä +3 p.: Osoita,
että verkko
ei ole planaarinen. (Bonustehtävä +3 p.: Osoita,
että verkko 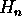 on planaarinen, jos ja vain jos
on planaarinen, jos ja vain jos 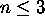 .)
.)
(Huomautus: Hyperkuution ![]() Hamiltonin syklit vastaavat
kokonaislukujen 0, ...,
Hamiltonin syklit vastaavat
kokonaislukujen 0, ..., ![]() ns. syklisiä Gray-koodeja,
joissa kahden peräkkäisen luvun binääriesitykset poikkeavat
aina vain yhdessä bitissä.)
ns. syklisiä Gray-koodeja,
joissa kahden peräkkäisen luvun binääriesitykset poikkeavat
aina vain yhdessä bitissä.)