-
Merkkijono x kuuluu kieleen EQUIV täsmälleen silloin, kun kaava
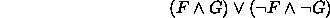
on tautologia eli kun kaava
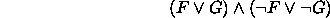
ei ole toteutuva.
Määritellään muunnos f asettamalla
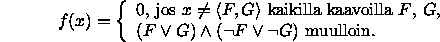
Tällöin
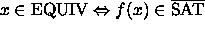 .
Muunnos f on polynomisessa ajassa laskettava, joten EQUIV
.
Muunnos f on polynomisessa ajassa laskettava, joten EQUIV 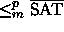 .
.
Kieliluokka co-NP on suljettu polynomisessa ajassa laskettavien muunnosten suhteen (harjoitus 2, tehtävä 4 b). Koska SAT
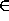 NP,
NP, 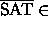 co-NP
ja myös EQUIV
co-NP
ja myös EQUIV 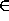 co-NP =
co-NP = 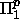 .
. -
Kieleen B kuulukoot syntaktisesti kelvolliset lausekalkyylin kaavat. Tämä
kieli tunnistetaan
polynomisessa ajassa, siis B
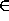 P.
P.
Helposti nähdään, että MINIM = B

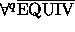 polynomilla
q(n) = n - 1:
polynomilla
q(n) = n - 1:
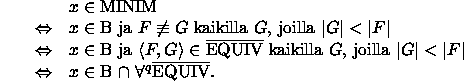
Koska EQUIV
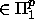 ,
, 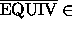 co-
co- 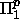 =
= 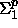 ja MINIM
ja MINIM 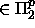 .
.
-
Olkoon NP suljettu pT-palautusten suhteen, ts. jos
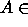 NP ja
NP ja 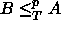 ,
niin myös
,
niin myös 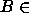 NP.
NP.
Olkoon
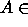 NP. Tällöin lauseen 3.2 kohtien
NP. Tällöin lauseen 3.2 kohtien
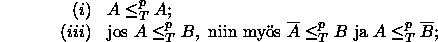
perusteella
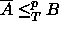 ja oletuksen mukaan
ja oletuksen mukaan 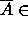 NP.
Näin nähdään, että NP = co-NP.
NP.
Näin nähdään, että NP = co-NP. -
Olkoon NP = co-NP.
Olkoon
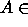 NP ja
NP ja 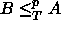 . Tällöin
. Tällöin 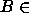 P(A) eli kieli
B
tunnistetaan deterministisesti polynomisessa ajassa jollakin
oraakkelikoneella M
ja oraakkelilla A. Korvataan M:n tilassa
P(A) eli kieli
B
tunnistetaan deterministisesti polynomisessa ajassa jollakin
oraakkelikoneella M
ja oraakkelilla A. Korvataan M:n tilassa 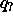 tapahtuva oraakkelikysely
kielet
A ja
tapahtuva oraakkelikysely
kielet
A ja 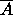 tunnistavien epädeterminististen Turingin koneiden
N ja N'
simuloinnilla seuraavasti:
tunnistavien epädeterminististen Turingin koneiden
N ja N'
simuloinnilla seuraavasti:
Ensin simuloidaan konetta N oraakkelinauhalla olevalla syötteellä. Jos N hyväksyy syötteen, jatketaan M:n tilasta
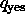 . Jos N
hylkää syötteen,
syöte voi silti kuulua kieleen A. Silloin simuloidaan konetta N'
oraakkelinauhalla
olevalla syötteellä. Jos N hyväksyy syötteen, jatketaan M:n tilasta
. Jos N
hylkää syötteen,
syöte voi silti kuulua kieleen A. Silloin simuloidaan konetta N'
oraakkelinauhalla
olevalla syötteellä. Jos N hyväksyy syötteen, jatketaan M:n tilasta
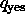 . Jos N hylkää syötteen, jatketaan M:n tilasta
. Jos N hylkää syötteen, jatketaan M:n tilasta
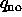 .
.
Modifioitu M toimii ekvivalentisti alkuperäisen M:n kanssa epädeterministisenä Turingin koneena, joka tunnistaa kielen B polynomisessa ajassa, sillä M tekee oraakkelikyselyjä polynomisen määrän, joihin N ja N' antavat vastauksen polynomisessa ajassa. Näin nähdään, että NP on suljettu pT-palautusten suhteen.
- Olkoon
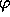 (mahdollisesti kvantifioitu) lausekalkyylin kaava ja
x jokin tässä
kaavassa esiintyvä muuttuja. Merkitään
(mahdollisesti kvantifioitu) lausekalkyylin kaava ja
x jokin tässä
kaavassa esiintyvä muuttuja. Merkitään 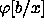 :llä kaavaa, joka
saadaan
:llä kaavaa, joka
saadaan 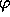 :stä
sijoittamalla x:lle arvo
:stä
sijoittamalla x:lle arvo 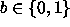 ja sieventämällä. Voidaan
todeta, että aina on
ja sieventämällä. Voidaan
todeta, että aina on
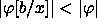 . Tämän perusteella saadaan kielille SAT ja QBF
seuraavat
itsepalautusalgoritmit:
. Tämän perusteella saadaan kielille SAT ja QBF
seuraavat
itsepalautusalgoritmit:
SAT(
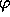 ):
):
-
Jos
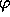 :ssä ei ole yhtään muuttujaa, määritä sen vakioarvo; jos
:ssä ei ole yhtään muuttujaa, määritä sen vakioarvo; jos
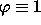 ,
niin hyväksy, muuten hylkää.
,
niin hyväksy, muuten hylkää. -
Muuten olkoon x jokin
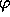 :n muuttuja. Määritä oraakkelikutsuilla
totuusarvot
:n muuttuja. Määritä oraakkelikutsuilla
totuusarvot
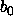 ja
ja 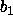 :
:


Jos
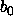 = 1 tai
= 1 tai 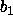 = 1, niin hyväksy, muuten hylkää.
= 1, niin hyväksy, muuten hylkää.
QBF(
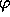 ):
):
-
Jos kaava
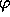 on kvanttoriton, määritä sen arvo suoraan.
on kvanttoriton, määritä sen arvo suoraan. -
Muuten on kaksi tapausta:
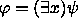 ja
ja 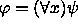 jollakin kaavalla
jollakin kaavalla 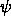 . Määritä oraakkelikutsuilla totuusarvot
. Määritä oraakkelikutsuilla totuusarvot 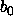 ja
ja
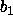 :
:


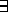 -tapauksessa palauta tulos
-tapauksessa palauta tulos 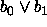 ,
, 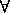 -tapauksessa
-tapauksessa
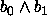 .
.
-
Jos
-
Väite. Jos kieli A on itsepalautuva, niin
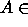 PSPACE.
PSPACE.
Todistus. Olkoon A = L(M, A), missä M on polynomisessa ajassa p(n) toimiva oraakkelikone.
Konetta M voidaan ajatella myös ``rekursiivisena ohjelmana'' ja simuloida sen toimintaa pinon avulla: aina kun M syötteellä x tekee oraakkelikyselyn jonosta y, |y| < |x|, talletetaan M:n kyselyhetkinen tilanne pinoon ja käynnistetään uusi M:n laskenta syötteellä y. Tällöin syötteellä x, jonka pituus on n, pinossa voi kerrallaan olla enintään n talletettua tilannetta, kukin kooltaan O(p(n)) merkkiä. Siten konetta M voidaan simuloida tilassa O(np(n)).
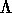
![]()
löytämät merkkeihin ![]() johtavat laskennat kuuluvat epädeterministisen
koneen tilannepuun
eri polkuihin, mikä ei takaa, että olisi olemassa jokin polku, joka tuottaa
yhtä aikaa kaikki
merkit
johtavat laskennat kuuluvat epädeterministisen
koneen tilannepuun
eri polkuihin, mikä ei takaa, että olisi olemassa jokin polku, joka tuottaa
yhtä aikaa kaikki
merkit ![]() . Siksi tällä menetelmällä ei voida todistaa, että
NTIME
. Siksi tällä menetelmällä ei voida todistaa, että
NTIME ![]() ASPACE(s(n)).
ASPACE(s(n)).
Todistus. Olkoon ![]() 0. Jos vaihdetaan keskenään
0. Jos vaihdetaan keskenään
![]() -koneen hyväksyvät ja
hylkäävät tilat sekä eksistentiaaliset ja universaaliset tilat, saadaan
-koneen hyväksyvät ja
hylkäävät tilat sekä eksistentiaaliset ja universaaliset tilat, saadaan
![]() -kone, joka
tunnistaa alkuperäisen koneen tunnistaman kielen komplementin. Siten
väitteen
-kone, joka
tunnistaa alkuperäisen koneen tunnistaman kielen komplementin. Siten
väitteen ![]() P =
P =
![]() todistaminen riittää, koska silloin
todistaminen riittää, koska silloin ![]() P = co-
P = co- ![]() P =
co-
P =
co- ![]() =
= ![]() .
.
Väite on tosi indekseillä k = 0 ja k = 1, sillä ![]() -kone on
deterministinen Turingin kone
ja
-kone on
deterministinen Turingin kone
ja ![]() -kone on epädeterministinen Turingin kone, ja siten
-kone on epädeterministinen Turingin kone, ja siten
![]() =
= ![]() = P
=
= P
= ![]() P =
P = ![]() P,
P, ![]() = NP =
= NP = ![]() P ja
P ja ![]() =
co-NP =
=
co-NP = ![]() P.
P.
Olkoon ![]() 1. Oletetaan, että
1. Oletetaan, että ![]() P =
P = ![]() ja
ja
![]() P =
P = ![]() (induktio-oletus).
(induktio-oletus).
-
Olkoon
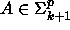 . Osoitetaan, että
. Osoitetaan, että 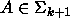 P.
P.
Nyt
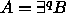 jollakin polynomilla q, missä kieli B kuuluu
luokkaan
jollakin polynomilla q, missä kieli B kuuluu
luokkaan 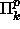 ,
joka on induktio-oletuksen mukaan sama kuin luokka
,
joka on induktio-oletuksen mukaan sama kuin luokka 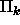 P. Olkoon M
kielen B
polynomisessa ajassa tunnistava
P. Olkoon M
kielen B
polynomisessa ajassa tunnistava 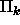 -kone.
-kone.
Alternoiva eksistentiaalisessa tilassa aloittava Turingin kone N generoikoon epädeterministisesti kaikki merkkijonot y, joilla
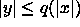 ,
ja testatkoon
merkkijonon
,
ja testatkoon
merkkijonon 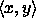 kuulumisen kieleen B kuten M. Jos M
hyväksyy
kuulumisen kieleen B kuten M. Jos M
hyväksyy
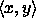 :n jollakin y, niin N hyväksyy, muuten hylkää
x:n.
:n jollakin y, niin N hyväksyy, muuten hylkää
x:n.
Kone N tunnistaa kielen
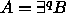 , sillä
, sillä
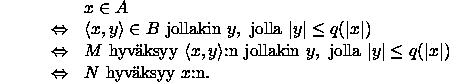
Kielen A tunnistaminen koneella N tapahtuu polynomisessa ajassa, sillä syötteellä x merkkijonon
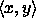 muodostaminen ja testaaminen kieleen B
kuuluvaksi
konetta M simuloiden tapahtuvat polynomisessa ajassa.
muodostaminen ja testaaminen kieleen B
kuuluvaksi
konetta M simuloiden tapahtuvat polynomisessa ajassa.
Kone N alternoi tasan yhden kerran useammin kuin M, joka alternoi enintään k - 1 kertaa, joten N alternoi enintään k kertaa. Alkutilan mukaan N on
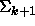 -kone.
-kone.
Koska kieli A tunnistetaan polynomisessa ajassa
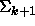 -koneella,
-koneella,
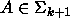 P.
P. -
Olkoon sitten
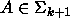 P.
Osoitetaan, että
P.
Osoitetaan, että 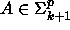 .
.
Olkoon M polynomisessa ajassa q kielen A tunnistava
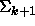 -kone.
Määritellään Continue
-kone.
Määritellään Continue 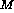 kieleksi, johon kuuluvat koneen M hyväksymiseen
johtavat
universaaliset tilanteet
kieleksi, johon kuuluvat koneen M hyväksymiseen
johtavat
universaaliset tilanteet 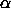 , joista lähtien M pysähtyy ajassa
, joista lähtien M pysähtyy ajassa
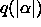 ja alternoi enintään k - 1 kertaa. Saavutettavasta tilanteesta alkava
M:n laskenta
pysähtyy vaaditussa ajassa ja sallituilla alternaatioilla, joten
Continue
ja alternoi enintään k - 1 kertaa. Saavutettavasta tilanteesta alkava
M:n laskenta
pysähtyy vaaditussa ajassa ja sallituilla alternaatioilla, joten
Continue 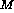 sisältää
kaikki saavutettavat hyväksymiseen johtavat universaaliset tilanteet.
sisältää
kaikki saavutettavat hyväksymiseen johtavat universaaliset tilanteet.
Kieli Continue
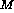 tunnistetaan alternoivalla Turingin koneella N, jonka
alkutila on
universaalinen. Tämä kone tarkistaa, että syöte on syntaktisesti
kelvollinen, kirjoittaa annetun
tilanteen
tunnistetaan alternoivalla Turingin koneella N, jonka
alkutila on
universaalinen. Tämä kone tarkistaa, että syöte on syntaktisesti
kelvollinen, kirjoittaa annetun
tilanteen 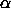 nauhasisällöt työnauhoilleen, siirtää nauhapäät
tilannetta
nauhasisällöt työnauhoilleen, siirtää nauhapäät
tilannetta 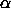 vastaavaan kohtaan ja simuloi sitten konetta M jatkaen laskentaa
tilanteeseen
vastaavaan kohtaan ja simuloi sitten konetta M jatkaen laskentaa
tilanteeseen 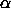 kuuluvassa koneen tilassa. Koneen N laskenta-aikaa rajoitetaan laskurilla,
jonka
alkuarvoksi asetetaan
kuuluvassa koneen tilassa. Koneen N laskenta-aikaa rajoitetaan laskurilla,
jonka
alkuarvoksi asetetaan 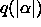 ja jota vähennetään yhdellä jokaisen
simulointiaskelen
jälkeen. Jos laskuri nollautuu, N hylkää syötteen.
ja jota vähennetään yhdellä jokaisen
simulointiaskelen
jälkeen. Jos laskuri nollautuu, N hylkää syötteen.
Koneen M alternaatioita seuraava kone N alternoi enintään k - 1 kertaa. Alkutilan mukaan N on
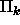 -kone.
-kone.
Kone N tunnistaa kielen Continue
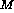 polynomisessa ajassa, sillä syötteen
tarkistaminen
ja siirtäminen työnauhoille sekä jatkolaskenta konetta M aikarajoitetusti
simuloiden
tapahtuvat polynomisessa ajassa. Koska N on
polynomisessa ajassa, sillä syötteen
tarkistaminen
ja siirtäminen työnauhoille sekä jatkolaskenta konetta M aikarajoitetusti
simuloiden
tapahtuvat polynomisessa ajassa. Koska N on 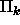 -kone, kieli
Continue
-kone, kieli
Continue 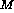 kuuluu
luokkaan
kuuluu
luokkaan 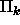 P, joka on induktio-oletuksen mukaan sama kuin luokka
P, joka on induktio-oletuksen mukaan sama kuin luokka
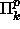 .
.
Määritellään kielet

Nyt pätee
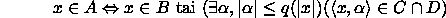
eli
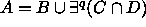 jollakin polynomilla q.
jollakin polynomilla q.
Kieli B tunnistetaan epädeterministisesti polynomisessa ajassa, joten
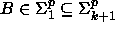 . Koska
. Koska 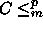 Continue
Continue 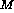
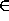
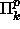 , myös
, myös
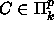 . Kieli D tunnistetaan epädeterministisesti polynomisessa
ajassa koneella,
joka tarkistaa syötteen olevan muotoa
. Kieli D tunnistetaan epädeterministisesti polynomisessa
ajassa koneella,
joka tarkistaa syötteen olevan muotoa 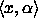 , simuloi
konetta M syötteellä
x ensimmäiseen alternaatioon saakka ja tällöin vertaa
, simuloi
konetta M syötteellä
x ensimmäiseen alternaatioon saakka ja tällöin vertaa 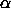 :aa
saavutettuun tilanteeseen.
Tämä kone hylkää syötteet, joilla laskenta päättyy ennen M:n ensimmäistä
alternaatiota.
:aa
saavutettuun tilanteeseen.
Tämä kone hylkää syötteet, joilla laskenta päättyy ennen M:n ensimmäistä
alternaatiota.
Tiedetään, että
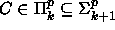 ja
ja 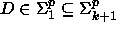 . Siten
. Siten 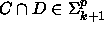 ja, koska
ja, koska
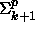 on
suljettu polynomirajoitetun eksistenssikvantifioinnin suhteen, myös
on
suljettu polynomirajoitetun eksistenssikvantifioinnin suhteen, myös
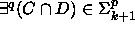 ja edelleen
ja edelleen 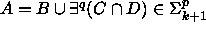 .
.
Todistus. Selvästi ![]() P =
P = ![]() .
.
Olkoon A = L(M), missä M on ![]() -kone, time
-kone, time ![]() ,
q polynomi.
Tällöin kuvaus
,
q polynomi.
Tällöin kuvaus
![]()
on polynomisessa ajassa laskettava palautus kielestä A kieleen ![]() .
.
![]()