Algoritmiteorian jatkokurssi, kevät 1999
Harjoitus 3, 19.4. klo 10-12 sali MaD380

1. 1. Osoita, että kieli

      

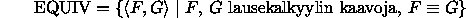
      kuuluu luokkaan 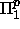= co-NP. (Merkintä `` 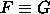'' tarkoittaa, että kaavat toteutuvat täsmälleen samoilla muuttujien totuusarvoasetuksilla.)

   2. Osoita edellisen nojalla, että kieli

      

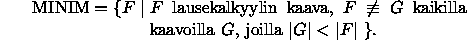
      kuuluu luokkaan 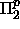. (Lisätieto: Kieli MINIM on itse asiassa 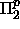-täydellinen.)

2. Osoita, että luokka NP on suljettu pT-palautusten suhteen, jos ja vain jos NP = co-NP.
3. Kieli A on itsepalautuva (engl. ``self-reducible''), jos on olemassa polynomisessa ajassa toimiva oraakkelikone M, jolla

   (i)

   A = L(M,A);

   (ii)

   kullakin syötteellä x kone M tekee oraakkelikyselyjä vain merkkijonoista y, joilla |y| < |x|.

   Osoita, että
   1. kielet SAT ja QBF ovat itsepalautuvia;
   2. jokainen itsepalautuva kieli kuuluu luokkaan PSPACE.
4. Miksi luentojen lauseen 4.10 (`` '') todistus edellyttää, että simuloitava kone on deterministinen (eikä esim. epädeterministinen)?

   KÄÄNNÄ

5. Alternoiva Turingin kone on -kone ( -kone), , jos sen alkutila on eksistentiaalinen (universaalinen), ja missä tahansa koneen laskennassa (so. millä tahansa laskentapolulla) koneen tila vaihtuu eksistentiaalisesta universaaliseksi tai toisinpäin (kone ``alternoi'') enintään k-1 kertaa. Lisäksi voidaan deterministisiä koneita sanoa - tai -koneiksi. Määritellään vaativuusluokat:

   

   Osoita, että kaikilla on ja . (Ohje: Todistus induktiolla k:n suhteen. Induktioaskelta varten tarkastele mielivaltaisen polynomisessa ajassa toimivan -koneen M tunnistamaa kieltä A, ja sen rinnalla kieltä

   

   Totea, että kieli kuuluu luokkaan , ja että väite seuraa tästä pienillä lisätarkasteluilla. Huom.: Vastaavalla argumentilla voidaan osoittaa, että Savitchin lauseen seurauksena on

   

   kaikilla .)

6. Osoita, että kaikilla seuraava kieli on -täydellinen:

   

   Lisätieto (ei tarvitse todistaa): Jonkin verran luonnollisempi -täydellisten kielten perhe on: