


Next: About this document
Up: No Title
Previous: No Title
-
Palautetaan mieleen, että funktio
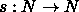 on
tilakonstruoituva, jos jollakin deterministisellä moninauhaisella
Turingin koneella
M on voimassa:
on
tilakonstruoituva, jos jollakin deterministisellä moninauhaisella
Turingin koneella
M on voimassa: 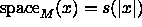 kaikilla syötejonoilla x.
Todista seuraavat väitteet:
kaikilla syötejonoilla x.
Todista seuraavat väitteet:
- Funktiot s(n) = k (vakio), s(n) = n ja
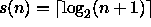 ovat tilakonstruoituvia.
ovat tilakonstruoituvia. - Jos
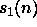 ja
ja 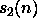 ovat tilakonstruoituvia, niin
myös
ovat tilakonstruoituvia, niin
myös 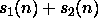 ,
, 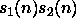 ja
ja 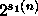 ovat tilakonstruoituvia.
ovat tilakonstruoituvia. - Jokaisella rekursiivisella funktiolla r(n) on olemassa
tilakonstruoituva
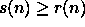 .
.
-
Todista, että jokaisella tilakonstruoituvalla
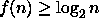 on voimassa sisältyvyys
on voimassa sisältyvyys
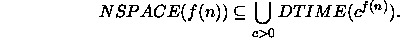
(Vihje: Muodosta verkko, jonka solmut ovat simuloitavan
epädeterministisen koneen tilannekuvauksia.)
-
Todista seuraava väite: Olkoon
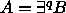 (
( 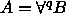 ),
missä q on polynomi ja
),
missä q on polynomi ja 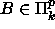 (
( 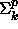 ),
), 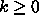 .
Olkoon
.
Olkoon 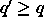 toinen polynomi.
Tällöin on olemassa
toinen polynomi.
Tällöin on olemassa 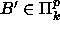 (
( 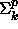 ), jolla
), jolla
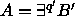 (
( 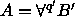 ).
). -
Todista, että polynomisen aikavaativuushierarkian luokilla
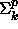 ,
,
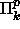 ,
, 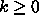 on seuraavat
sulkeumaominaisuudet (luentomuistiinpanojen Lause 2.8, s. 13):
on seuraavat
sulkeumaominaisuudet (luentomuistiinpanojen Lause 2.8, s. 13):
- Jos
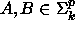 (
( 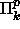 ), niin
), niin 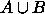 ,
,
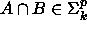 (
( 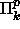 ).
). - Jos
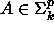 (
( 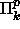 ) ja
) ja 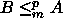 , niin
, niin 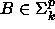 (
( 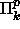 ).
). - Jos
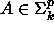 (
( 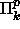 ),
), 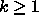 , ja
, ja
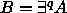 (
( 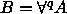 ), q polynomi,
niin
), q polynomi,
niin 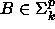 (
( 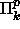 ).
).
(Sovitaan täsmällisyyden vuoksi, että polynomisen hierarkian
luokkien määrittelyssä käytetään parikoodausfunktiota
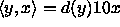 , missä
, missä 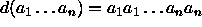 ,
ja tästä edelleen johdettua jonokoodausfunktiota
,
ja tästä edelleen johdettua jonokoodausfunktiota
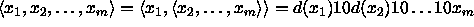 .)
.)
Huom.:
Pääsiäisloman takia kurssilla ei ole ohjelmaa 5.4. eikä 7.4. Seuraavat
demot ja luennot ovat maanantaina 12.4.
Pekka Orponen
Thu Apr 1 19:47:38 EET DST 1999
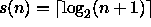 ovat tilakonstruoituvia.
ovat tilakonstruoituvia.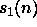 ja
ja 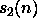 ovat tilakonstruoituvia, niin
myös
ovat tilakonstruoituvia, niin
myös 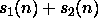 ,
, 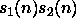 ja
ja 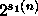 ovat tilakonstruoituvia.
ovat tilakonstruoituvia.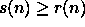 .
.
![]()
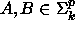 (
( 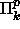 ), niin
), niin 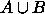 ,
,
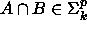 (
( 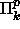 ).
).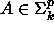 (
( 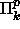 ) ja
) ja 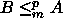 , niin
, niin 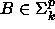 (
( 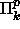 ).
).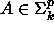 (
( 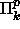 ),
), 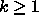 , ja
, ja
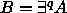 (
( 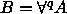 ), q polynomi,
niin
), q polynomi,
niin 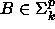 (
( 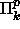 ).
).