TIE310 Algoritmien teoria (3 ov)
Loppukoe ke 16.6.1999 klo 8-12

1. Järjestä seuraavat funktiot kertaluokkiensa mukaiseen järjestykseen: n, 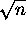, , 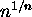, , 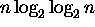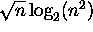2/n, , .
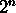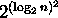2. Selitä ns. splay-puiden lisäysoperaation toiminta. Esitä puun rakenteen kehitys, kun aluksi tyhjään puuhun lisätään järjestyksessä alkiot 2, 1, 4, 6, 3, 5.
3. NP-täydellisessä ``riippumaton joukko''-ongelmassa tehtävänä on löytää annetusta suuntaamattomasta verkosta G mahdollisimman suuri joukko solmuja, joiden välillä ei kulje yhtään kaarta. Suunnittele ongelmalle jokin ``järkevä'' polynomisessa ajassa toimiva approksimointialgoritmi, ja anna esimerkki verkosta G, jossa algoritmisi ei löydä maksimaalisen suurta riippumatonta joukkoa. (Bonus 2 p.: Anna esimerkki verkosta, jossa algoritmisi löytämä joukko on kooltaan alle puolet maksimaalisesta.)
4. Henkilö A, joka kuuluu n:n ihmisen joukkoon, on julkkis, jos kaikki joukossa tuntevat A:n mutta A ei tunne muita. Tehtävänä on selvittää, onko annetussa joukossa julkkis ja kuka hän on, esittämällä yhdelle henkilölle kerrallaan kysymys ``Tunnetko tuon henkilön?''. Suunnittele algoritmi, joka ratkaisee tehtävän mahdollisimman vähillä kysymyksillä. (Vihje: Muotoile tehtävä verkko-ongelmana.)

Pisteytys: Kukin tehtävä 15 pistettä, yhteensä 60 pistettä.