TIE310 Algoritmien teoria (3 ov)
Loppukoe ke 5.5.1999 klo 8-12

1. Kumpi funktioist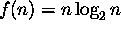a ja 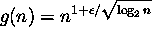, missä 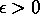, kasvaa asymptoottisesti nopeammin? (Perusteltu vastaus.)
2. Esitä NP-täydelliselle solmupeiteongelmalle polynomisessa ajassa toimiva approksimointialgoritmi, jonka tuottama solmupeite on aina enintään kaksi kertaa minimipeitteen kokoinen. Todista algoritmiin liittyvä em.\ approksimointitakuutulos.
3. Suunnittele tehokas algoritmi, joka etsii annetusta yhtenäisestä suuntaamattomasta verkosta solmun, joka ei ole verkon artikulaatiopiste, so. solmun jonka poistaminen ei riko verkon yhtenäisyyttä. Algoritmisi tulee olla yksinkertaisempi kuin luentomonisteessa esitetyn yleisen artikulaatiopisteiden määrittämisalgoritmin.
4. Tason pistejoukon A piste p = (x,y) on maksimaalinen, jos jokaisella A:n pisteellä p' = (x',y'), 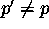, on joko x' < x tai y' < y (tai molemmat). Suunnittele ja analysoi tehokas algoritmi, joka määrittää syötteenä annetun äärellisen pistejoukon A kaikki maksimaaliset pisteet.

Pisteytys: Kukin tehtävä 15 pistettä, yhteensä 60 pistettä.