Algoritmien teoria, kevät 1999
Harjoitus 9, 22.3. klo 10-12 sali MaD380

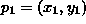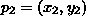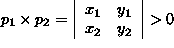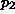1. Osoita, suoraan koordinaattiesityksiä tarkastelemalla, että jos ja ovat tason pisteitä, niin , jos ja vain jos piste on origosta katsoen vastapäivään pisteestä .
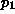2. Tehtävänä on laatia algoritmi, joka tutkii muodostaako annettu pistejono 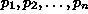järjestyksessä konveksin monikulmion kulmapisteet. Yksi idea olisi tarkastaa, että pistejonon määrittämän murtoviivan käännökset ovat joko kaikki vasempaan tai kaikki oikeaan. Mikä vika tässä ideassa on? Anna oikea, pistejonon pituuden suhteen lineaarisessa ajassa toimiva algoritmi.
3. Suunnittele tehokas algoritmi sen tutkimiseen, menevätkö kaksi kulmapistejonoina esitettyä yksinkertaista monikulmiota päällekkäin. (Monikulmio on yksinkertainen, jos se on yhtenäinen eivätkä sen sivut leikkaa toisiaan.)
4. Todista, että n-solmuisessa tasoverkossa (siis esimerkiksi n pisteen Delaunayn kolmioinnissa) voi olla enintään 3n-6 kaarta, kun 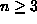. (Ohje: Todista ensin Eulerin kaava, jonka mukaan n-solmuisessa yhtenäisessä tasoverkossa, jossa on m kaarta ja p tahkoa (engl. faces), on voimassa yhtälö n-m+p=2. [Huomaa, että verkon ``ulkopuoli'' lasketaan myös tahkoksi.] Tämän kaavan todistus on induktio m:n suhteen: kullakin m:n arvolla tarkastellaan ensin erikseen tapaus, jossa verkko on syklitön, so. puu, ja sitten palautetaan syklin sisältävä verkko yksinkertaisempaan poistamalla syklistä yksi kaari. Haluttu tulos seuraa Eulerin kaavasta, kun ensin arvioidaan kaarien määrälle alaraja tahkojen määrän funktiona.)
5. Olkoon annettuna tason pistejoukko S. Suunnittele tehokas algoritmi, joka sijoittaa tasoon uuden pisteen siten, että se sijoittuu S:n konveksin verhon sisään, mutta on maksimaalisen kaukana kaikista S:n pisteistä. (Vihje: Sovella Voronoin kaavioita.)