Algoritmien teoria, kevät 1999
Harjoitus 8, 15.3. klo 10-12 sali MaD380

1. Osoita, että jos p>2 on alkuluku, niin kaikilla a, , on voimassa . (Vrt. luentomuistiinpanojen s. 222.) Käytä hyväksesi seuraavia algebrallisia perustietoja:
   1. Jos p on alkuluku, niin nollasta poikkeavien kokonaislukujen 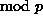muodostama ryhmä 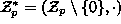on syklinen, so. jollakin alkiolla 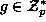on .
   2. Kaikilla a, 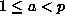, on 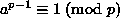(ns. Fermat'n pieni lause).
2. Testaa luennolla (s. 225) esitetyllä Solovayn-Strassenin algoritmilla ainakin 75% varmuudella, onko 103 alkuluku. (Huom: Luentomuistiinpanoissa on valitettavasti virhe s. 224 kohdassa (d): Gaussin resiprookkilause t. ``neliönjäännösten käännösyhtälö'' pätee vain, kun Jacobin symbolissa luvut y ja x ovat parittomia ja keskenään jaottomia. Jos symbolin ``osoittaja'' y on parillinen, voidaan sen sijaan soveltaa symbolin multiplikatiivisuuteen perustuvaa sääntöä .)
3. Johda luentomuistiinpanojen s. 233 esitetty, simuloidun jäähdytyksen asymptoottista konvergenssia kun koskeva Seurauslause 2 samalla sivulla esitetystä, algoritmin käyttäytymistä vakiolämpötilassa T > 0 koskevasta Lauseesta 1.
4. Tarkastellaan seuraavaa yksinkertaista ``säämallia''. Säätila annettuna päivänä voi olla joko aurinkoinen (a), pilvinen (p) tai sateinen (s). Seuraavan päivän säätilan todennäköisyysjakauma riippuu edellisen päivän säätilasta seuraavan siirtymämatriisin esittämällä tavalla (rivi-indeksi kuvaa päivän t, sarakeindeksi päivän t+1 säätilaa):

   

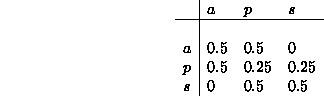
   Totea, että matriisin määrittelemällä ``sääprosessilla'' on tasapainojakauma, ja määritä se.

5. Hahmottele simuloitua jäähdytystä käyttävä ratkaisumenetelmä NP-täydelliselle solmupeiteongelmalle (engl. VERTEX COVER; luentomuistiinpanojen s. 117). Valitse sopiva kustannusfunktio ja naapurustorakenne. Varmista, että osaat tuottaa annetun kelvollisen ratkaisun satunnaisia naapuriratkaisuja tasaisen jakauman mukaan. Minkälaista jäähdytysaikataulua ongelman ratkaisemiseen n solmun verkossa tulisi käyttää luennolla esitetyn konvergenssilauseen 3 (s. 244) mukaan?