Algoritmien teoria, kevät 1999
Harjoitus 7, 8.3. klo 10-12 sali MaD380

1. Sanotaan, että Monte Carlo -tyyppinen satunnaisalgoritmi A on luotettava, jos se annetulla syötteellä antaa oikean vastauksen todennäköisyydellä p > 0, ja todennäköisyydellä q = 1-p vastaa ``en tiedä''. Mikä on oikean vastauksen todennäköisyys, kun algoritmi A suoritetaan k kertaa peräkkäin? (Oletetaan, että suorituskerrat ovat toisistaan riippumattomia, ja toisto lopetetaan heti kun oikea vastaus on saatu.) Montako kertaa algoritmia tarvitsee enintään toistaa, jotta oikean vastauksen todennäköisyys saataisiin suuremmaksi kuin , jollakin annetulla ?

2. Muodostetaan edellisen tehtävän algoritmin A pohjalta Las Vegas -tyyppinen algoritmi B, joka toistaa A:ta, kunnes saa oikean vastauksen (so. A vastaa jotakin muuta kuin ``en tiedä''). Mikä on tarvittavien toistojen määrän odotusarvo?
3. Olkoon A jonkin päätösongelman ratkaiseva (so. 0/1-arvoinen) Monte Carlo -algoritmi, joka antaa oikean vastauksen todennäköisyydellä p > 1/2 ja väärän vastauksen todennäköisyydellä q = 1-p. (Tällä kertaa algoritmi ei siis vastaa luotettavasti ``en tiedä'', vaan saattaa suorastaan valehdella.) Muodostetaan algoritmista A algoritmi B, joka toistaa A:ta k = 2t-1 kertaa ja valitsee vastaukseksi sen, jonka A antoi useammin, so. vähintään t kertaa. Arvioi todennäkoisyyttä, että B antaa väärän vastauksen, kun A:n eri suorituskerrat ovat toisistaan riippumattomia. Erityisesti: monellako A:n toistolla saadaan väärän vastauksen todennäköisyys pienemmäksi kuin jokin annettu ? (Käytä luentomuistiinpanojen s. 209 esitettyjä Chernoffin rajoja.)
4. Todista seuraavat hyppylistojen ominaisuudet:
   1. n alkion hyppylistan alkioiden maksimikorkeus on ``suurella todennäköisyydellä'' enintään .
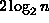   2. Kahden korkeutta h olevan alkion välissä on odotusarvoisesti O(1) korkeutta h-1 olevaa alkiota. (Vihje: Huomaa, että jos alkion x korkeus on vähintään h-1, niin todennäköisyydellä 1/2 sen korkeus on itse asiassa h tai suurempi.)
5. Lausekalkyylin kaava on disjunktiivisessa normaalimuodossa (dnf), jos se on muotoa

   

   missä kukin termi on literaalien konjunktio

   

   (Tässä siis kukin on joko muuttuja tai sellaisen negaatio.) Laadi satunnaisalgoritmi, joka arvioi monellako muuttujien totuusarvoasetuksella annettu dnf-muotoinen kaava tulee todeksi. (Idea: Kukin kaavan termi määrittelee tietyn toteuttavien totuusarvoasetusten joukon , ja koko kaavan toteuttavien asetusten joukko on näiden -joukkojen yhdiste. Sovella luentomuistiinpanojen s. 211 esitettyä joukkoyhdisteen kokoa arvioivaa satunnaisalgoritmia.) Lisätieto: Voidaan osoittaa, että jos P NP, niin toteuttavien asetusten määrää ei voida laskea tarkasti polynomisessa ajassa.