


Next: About this document
Up: No Title
Previous: No Title
-
Tarkastellaan kauppamatkustajan ongelmaa täydellisessä
verkossa G, jonka solmuina ovat tason pisteet (i,j),
missä i = 1,2,3 ja j = 1,2,3. Solmuja on siis yhdeksän
kappaletta. Solmujen välisten kaarten kustannukset ovat samat
kuin vastaavien pisteiden euklidiset etäisyydet.
Simuloi luennolla (muistiinpanojen ss. 143-146) esitettyjen kahden
 TSP-approksimointialgoritmin
(``kahdesti puun ympäri'' -tekniikka ja Christofidesin algoritmi)
toimintaa tässä verkossa. Kokeile kahta tai useampaa virittävää
puuta algoritmien lähtökohtana. Laske myös algoritmien tuottamien
ratkaisujen suhteelliset virheet.
TSP-approksimointialgoritmin
(``kahdesti puun ympäri'' -tekniikka ja Christofidesin algoritmi)
toimintaa tässä verkossa. Kokeile kahta tai useampaa virittävää
puuta algoritmien lähtökohtana. Laske myös algoritmien tuottamien
ratkaisujen suhteelliset virheet. -
Tarkastellaan seuraavaa solmupeiteongelman ahnetta
approksimointialgoritmia: Verkosta valitaan peitteeseen
lisättäväksi solmu, jonka asteluku on mahdollisimman suuri,
ja poistetaan kaikki siihen liittyvät kaaret.
Tätä toistetaan, kunnes verkossa ei ole enää kaaria jäljellä.
Osoita, että algoritmi voi pahimmassa tapauksessa valita peitteen C,
jolla
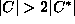 , missä
, missä 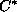 on optimipeite.
on optimipeite. -
Ratkaise repunpakkausongelma, jossa tavaroiden ``koot'' ovat
(4, 1, 2, 3, 2, 1, 2) ja ``arvot'' vastaavasti
(299, 73, 159, 221, 137, 89, 157) soveltamalla luennolla
(ss. 149-152) esitettyä
 -approksimointiskeemaa parametrin
-approksimointiskeemaa parametrin
 arvolla 1. Repun maksimikoko on 10.
arvolla 1. Repun maksimikoko on 10. -
Tarkastellaan seuraavaa NP-täydellistä lokerointiongelmaa
(engl. Bin Packing):
Annettu joukko välin (0,1) reaalilukuja 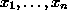 .
Luvut on ositettava mahdollisimman pieneen määrään osajoukkoja
(``lokeroita'') siten, että kunkin osajoukon alkioiden summa on
korkeintaan 1.
.
Luvut on ositettava mahdollisimman pieneen määrään osajoukkoja
(``lokeroita'') siten, että kunkin osajoukon alkioiden summa on
korkeintaan 1.
Ongelman ahne first fit-approksimointialgoritmi toimii
seuraavasti: Luvut käsitellään järjestyksessä 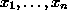 .
Luku
.
Luku 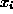 sijoitetaan lokeroiden järjestyksessä ensimmäiseen
lokeroon, johon se mahtuu. Osoita, että tämä menettely on
1-approksimointialgoritmi, so. tarvitsee enintään kaksinkertaisen
määrän lokeroita optimaaliseen nähden. (Vihje: Osoita, että
first fit-heuristiikka täyttää kaikki lokerot, paitsi
mahdollisesti yhden, ainakin puolilleen.)
sijoitetaan lokeroiden järjestyksessä ensimmäiseen
lokeroon, johon se mahtuu. Osoita, että tämä menettely on
1-approksimointialgoritmi, so. tarvitsee enintään kaksinkertaisen
määrän lokeroita optimaaliseen nähden. (Vihje: Osoita, että
first fit-heuristiikka täyttää kaikki lokerot, paitsi
mahdollisesti yhden, ainakin puolilleen.) -
Todista luennolla esitetty Seurauslause 7.1 (muistiinpanojen s. 153):
Jos P
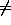 NP, niin luokassa NP
NP, niin luokassa NP 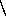 P on kieliä (ongelmia),
jotka eivät ole NP-täydellisiä.
P on kieliä (ongelmia),
jotka eivät ole NP-täydellisiä. -
-
Todista seuraava luennolla esitetyn Lauseen 7.8 (muistiinpanojen s. 154)
yleistys: Olkoon
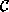 jokin kieliluokka (so. ongelmaluokka,
esim.
jokin kieliluokka (so. ongelmaluokka,
esim. 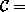 P, NP, PSPACE,...).
Kieli (ongelma) A on co-
P, NP, PSPACE,...).
Kieli (ongelma) A on co- 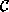 -täydellinen, jos ja vain jos sen
komplementtikieli
-täydellinen, jos ja vain jos sen
komplementtikieli 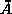 on
on 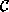 -täydellinen.
-täydellinen. -
Osoita tämän tuloksen perusteella, että lausekalkyylin kaavojen
tautologisuusongelma (muistiinpanojen s. 154) on co-NP-täydellinen.



Next: About this document
Up: No Title
Previous: No Title
Pekka Orponen
Wed Feb 24 15:02:49 EET 1999
. Luvut on ositettava mahdollisimman pieneen määrään osajoukkoja (``lokeroita'') siten, että kunkin osajoukon alkioiden summa on korkeintaan 1.
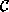 jokin kieliluokka (so. ongelmaluokka,
esim.
jokin kieliluokka (so. ongelmaluokka,
esim. 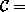 P, NP, PSPACE,...).
Kieli (ongelma) A on co-
P, NP, PSPACE,...).
Kieli (ongelma) A on co- 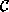 -täydellinen, jos ja vain jos sen
komplementtikieli
-täydellinen, jos ja vain jos sen
komplementtikieli 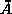 on
on 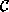 -täydellinen.
-täydellinen.