


Next: About this document
Up: No Title
Previous: No Title
-
Todista seuraavat yhtenäisen suuntaamattoman verkon G
artikulaatiopisteitä ja 2-yhtenäisiä komponentteja
koskevat väitteet (luentomuistiinpanojen s. 186):
- Kaaret
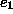 ja
ja 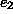 kuuluvat G:n samaan 2-yhtenäiseen
komponenttiin, jos ja vain jos
kuuluvat G:n samaan 2-yhtenäiseen
komponenttiin, jos ja vain jos 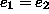 tai G:ssä on sykli
joka sisältää molemmat kaaret.
tai G:ssä on sykli
joka sisältää molemmat kaaret. - Kahdella G:n 2-yhtenäisellä komponentilla on enintään
yksi yhteinen solmu.
- G:n artikulaatiopisteet ovat täsmälleen sen 2-yhtenäisten
komponenttien leikkaussolmut.
-
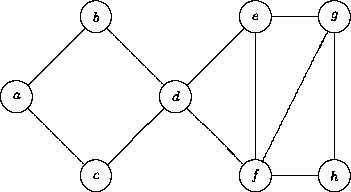
Määritä alla olevan verkon 2-yhtenäiset komponentit luennolla
esitetyllä algoritmilla (muistiinpanojen s. 189a). Oletetaan, että
solmut ovat vieruslistoissa aakkosjärjestyksessä ja että algoritmi
aloittaa verkon tutkimisen solmusta a.
-
Laadi algoritmi, joka tutkii onko syötteenä annettu
suuntaamaton verkko kaksijakoinen. Algoritmin tulee toimia
verkon kaarien määrän suhteen lineaarisessa ajassa. (Syöteverkon
solmuista ei siis ole valmiiksi sanottu, mitkä ovat jaon ``vasemmalla''
ja mitkä ``oikealla'' puolella. Huomaa kuitenkin, että
kaksijakoisuusehdon mukaan ``vasemman puolen'' solmuista voi olla
kaaria vain ``oikean puolen'' solmuihin ja päinvastoin.)
-
Binäärinen De Bruijnin jono on
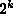 -bittinen binäärijono
-bittinen binäärijono
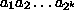 , joka syklisesti luettaessa sisältää kaikki
k-bittiset binäärijonot osajonoinaan. (Esimerkiksi 00010111 on
eräs De Bruijnin jono, missä k = 3.) Luonnostele algoritmi, joka
tuottaa n-bittisen De Bruijnin jonon, missä n on muotoa
, joka syklisesti luettaessa sisältää kaikki
k-bittiset binäärijonot osajonoinaan. (Esimerkiksi 00010111 on
eräs De Bruijnin jono, missä k = 3.) Luonnostele algoritmi, joka
tuottaa n-bittisen De Bruijnin jonon, missä n on muotoa 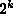 ,
n:n suhteen lineaarisessa ajassa. (Vihje: Tarkastele suunnattua
verkkoa
,
n:n suhteen lineaarisessa ajassa. (Vihje: Tarkastele suunnattua
verkkoa 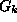 , jonka solmut vastaavat kaikkia mahdollisia
k-1-bittisiä binäärijonoja, ja solmusta
, jonka solmut vastaavat kaikkia mahdollisia
k-1-bittisiä binäärijonoja, ja solmusta 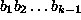 on
symboleilla 0 ja 1 nimetyt suunnatut kaaret solmuihin
on
symboleilla 0 ja 1 nimetyt suunnatut kaaret solmuihin 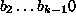 ja
ja 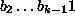 .)
.) -
Tarkastellaan seuraavaa ``edustajien valinta''-ongelmaa. Syötteenä
annetaan kokoelma perusjoukon
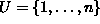 osajoukkoja
osajoukkoja
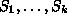 . Tehtävänä on valita kustakin joukosta alkio
. Tehtävänä on valita kustakin joukosta alkio
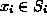 siten, että
siten, että 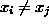 , kun
, kun 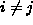 .
Hahmottele algoritmi edustajien valintaan. (Vihje:
Kaksijakoisten verkkojen pariutus.)
.
Hahmottele algoritmi edustajien valintaan. (Vihje:
Kaksijakoisten verkkojen pariutus.)
Pekka Orponen
Mon Mar 22 15:28:36 EET 1999
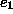 ja
ja 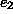 kuuluvat G:n samaan 2-yhtenäiseen
komponenttiin, jos ja vain jos
kuuluvat G:n samaan 2-yhtenäiseen
komponenttiin, jos ja vain jos 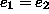 tai G:ssä on sykli
joka sisältää molemmat kaaret.
tai G:ssä on sykli
joka sisältää molemmat kaaret.