


Next: About this document
Up: No Title
Previous: No Title
-
-
Esitä binäärisen hakupuun päivitysalgoritmien toiminta, kun aluksi
tyhjään puuhun ensin lisätään alkiot 6, 2, 7, 0, 4, 5, 9, 8,
ja näin saadusta puusta sitten poistetaan alkio 2.
-
Osoita, että n alkion lisääminen aluksi tyhjään
binääriseen hakupuuhun vaatii pahimmassa tapauksessa
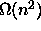 vertailuoperaatiota.
vertailuoperaatiota.
- Bonustehtävä.
Osoita, että vertailujen määrän odotusarvo, kun aluksi
tyhjään binääriseen hakupuuhun
lisätään n satunnaista alkiota, on
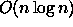 .
(Ohje: Olkoot lisättävät alkiot
.
(Ohje: Olkoot lisättävät alkiot 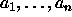 .
Puun juureen sijoittuva alkio
.
Puun juureen sijoittuva alkio 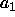 on todennäköisyydellä
on todennäköisyydellä
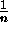 joukon k:nneksi pienin. Tässä tapauksessa
vasempaan alipuuhun sijoittuu k-1 alkiota ja oikeaan
alipuuhun n-k alkiota. Muodosta tältä pohjalta vertailujen
määrän odotusarvoa kuvaava rekursioyhtälö ja ratkaise se
joko arvauksen sovitusmenetelmällä tai ns. historian
eliminoinnilla (ks. pikalajittelualgoritmin analyysi,
muistiinpanojen s. 35).)
joukon k:nneksi pienin. Tässä tapauksessa
vasempaan alipuuhun sijoittuu k-1 alkiota ja oikeaan
alipuuhun n-k alkiota. Muodosta tältä pohjalta vertailujen
määrän odotusarvoa kuvaava rekursioyhtälö ja ratkaise se
joko arvauksen sovitusmenetelmällä tai ns. historian
eliminoinnilla (ks. pikalajittelualgoritmin analyysi,
muistiinpanojen s. 35).) -
-
Esitä (2,3)-puun päivitysalgoritmien toiminta, kun aluksi
tyhjään puuhun ensin lisätään alkiot 6, 2, 7, 0, 4, 5, 9, 8,
ja näin saadusta puusta sitten poistetaan alkio 0.
-
Osoita, että n alkion lisääminen aluksi tyhjään
(2,3)-puuhun vaatii enintään
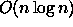 operaatiota.
operaatiota.
-
-
Esitä AVL-puun lisäysalgoritmin toiminta, kun aluksi
tyhjään puuhun lisätään alkiot 6, 2, 7, 0, 4, 5, 9, 8.
-
Suunnittele AVL-puille poistoalgoritmi ja esitä algoritmisi
toiminta, kun edellisessä tehtävässä muodostetusta puusta
poistetaan alkio 2.
-
Osoita, että AVL-puussa, jonka korkeus on h, on oltava
vähintään
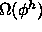 solmua, missä
solmua, missä 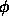 on ns.\
kultaisen leikkauksen suhde,
on ns.\
kultaisen leikkauksen suhde, 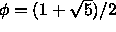 .
(Ohje:
Johda puun rakenteen perusteella rekursioyhtälö pienimmän
h:n korkuisen puun solmujen määrälle ja ratkaise se.)
Päättele tämän tiedon perusteella, että n-solmuisen
AVL-puun korkeus on luokkaa
.
(Ohje:
Johda puun rakenteen perusteella rekursioyhtälö pienimmän
h:n korkuisen puun solmujen määrälle ja ratkaise se.)
Päättele tämän tiedon perusteella, että n-solmuisen
AVL-puun korkeus on luokkaa 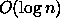 .
. -
Osoita, että universaalihajautusta käytettäessä minkä tahansa
avaimen x kanssa törmäävien muiden avainten
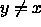 määrän
odotusarvo on alle 1 (vrt. Cormen/Leiserson/Rivest,
Introduction to Algorithms, ss. 230-231).
Päättele tästä, että hakemisto-operaatiot
MEMBER, INSERT ja DELETE voidaan universaalihajautusta käyttäen
toteuttaa odotusarvoisesti vakioajassa. (Huom. Odotusarvo
lasketaan siis hajautinten, ei syötteenä saatavien avainkokoelmien
suhteen. Kaikki avainkokoelmat ovat samassa asemassa.)
määrän
odotusarvo on alle 1 (vrt. Cormen/Leiserson/Rivest,
Introduction to Algorithms, ss. 230-231).
Päättele tästä, että hakemisto-operaatiot
MEMBER, INSERT ja DELETE voidaan universaalihajautusta käyttäen
toteuttaa odotusarvoisesti vakioajassa. (Huom. Odotusarvo
lasketaan siis hajautinten, ei syötteenä saatavien avainkokoelmien
suhteen. Kaikki avainkokoelmat ovat samassa asemassa.)



Next: About this document
Up: No Title
Previous: No Title
Pekka Orponen
Mon Mar 22 15:29:18 EET 1999
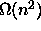 vertailuoperaatiota.
vertailuoperaatiota.
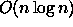 operaatiota.
operaatiota.