-
Määritä rekursioyhtälön
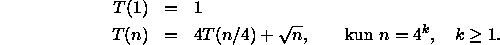
tarkka ratkaisu, kun n on neljän potenssi.
-
Eräissä ``hajota ja hallitse''-tyyppisissä algoritmeissa voidaan
n:n kokoinen ongelman tapaus osittaa tasaisesti
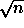 :n
kokoisiin osatapauksiin niin, että algoritmin aikavaativuutta
T(n) tulee kuvaamaan rekursiokaava:
:n
kokoisiin osatapauksiin niin, että algoritmin aikavaativuutta
T(n) tulee kuvaamaan rekursiokaava:
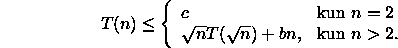
Määrää  -yläraja funktiolle T(n).
(Vihje: Tee muuttujanvaihto
-yläraja funktiolle T(n).
(Vihje: Tee muuttujanvaihto 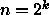 .)
.)
-
Ratkaise generoivia funktioita käyttäen rekursioyhtälö
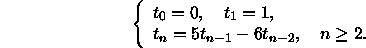
(Vihje: Kun olet määrittänyt jonon 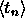 generoivan funktion,
yritä kirjoittaa sen nimittäjänä oleva lauseke muotoon
(1-az)(1-bz) ja sovella sitten osamurtolukuhajotelmaa.)
generoivan funktion,
yritä kirjoittaa sen nimittäjänä oleva lauseke muotoon
(1-az)(1-bz) ja sovella sitten osamurtolukuhajotelmaa.)
-
Tiedetään (Anal. pk/jk), että nollan ympäristössä suppeneva
potenssisarja voidaan derivoida termeittäin, so. jos
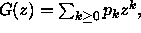 niin
niin
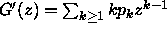 .
.
- Johda tämän tiedon avulla jonon
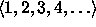 generoiva funktio jonon
generoiva funktio jonon 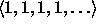 generoivasta
funktiosta.
generoivasta
funktiosta. - Oletetaan, että jonon
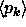 arvot ovat jonkin
diskreetin todennäköisyysjakauman pistetodennäköisyyksiä, siis
esim. ``
arvot ovat jonkin
diskreetin todennäköisyysjakauman pistetodennäköisyyksiä, siis
esim. `` 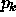 = todennäköisyys, että algoritmin suoritus
vaatii tasan k askelta''. Mitä on tällöin G(1)?
Entä mikä on arvon G'(1) tulkinta?
= todennäköisyys, että algoritmin suoritus
vaatii tasan k askelta''. Mitä on tällöin G(1)?
Entä mikä on arvon G'(1) tulkinta?
-
Ohjelma käsittelee kahta pinoa S ja T, joihin voidaan
tavallisten pino-operaatioiden (push, pop) lisäksi kohdistaa
kopiointi-operaatioita copy(S,T) ja copy(T,S).
Suunnittele pinoille taulukkototeutus, jossa kopiointi-operaation
yhteydessä ainoastaan edellisen kopioinnin jälkeen tapahtuneet
muutokset päivitetään pinosta toiseen.
Osoita, että tässä toteutuksessa minkä tahansa aluksi samansisältöisiin
pinoihin kohdistuvan n operaation jonon kokonaissuoritusaika on vain O(n).
![]()
![]()
![]() -yläraja funktiolle T(n).
(Vihje: Tee muuttujanvaihto
-yläraja funktiolle T(n).
(Vihje: Tee muuttujanvaihto ![]() .)
.)![]()
![]() generoivan funktion,
yritä kirjoittaa sen nimittäjänä oleva lauseke muotoon
(1-az)(1-bz) ja sovella sitten osamurtolukuhajotelmaa.)
generoivan funktion,
yritä kirjoittaa sen nimittäjänä oleva lauseke muotoon
(1-az)(1-bz) ja sovella sitten osamurtolukuhajotelmaa.)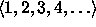 generoiva funktio jonon
generoiva funktio jonon 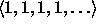 generoivasta
funktiosta.
generoivasta
funktiosta.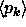 arvot ovat jonkin
diskreetin todennäköisyysjakauman pistetodennäköisyyksiä, siis
esim. ``
arvot ovat jonkin
diskreetin todennäköisyysjakauman pistetodennäköisyyksiä, siis
esim. `` 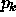 = todennäköisyys, että algoritmin suoritus
vaatii tasan k askelta''. Mitä on tällöin G(1)?
Entä mikä on arvon G'(1) tulkinta?
= todennäköisyys, että algoritmin suoritus
vaatii tasan k askelta''. Mitä on tällöin G(1)?
Entä mikä on arvon G'(1) tulkinta?