Proceedings of STeP'96. Jarmo Alander, Timo Honkela and Matti Jakobsson (eds.),
Publications of the Finnish Artificial Intelligence Society, pp. 25-34.
Structural Optimization of Feedforward Networks
Heikki Hyötyniemi
Helsinki University of Technology
Control Engineering Laboratory
Otakaari 5A, FIN-02150 Espoo, Finland
Abstract:
Optimizing the structure of a feedforward neural network is
studied actively, and many (more or less heuristic) approaches have been
proposed. This paper shows that the age-old methods based on
linear programming can be applied to reach fast and reliable
results.
A PostScript version of this paper is available also at
http://www.hut.fi/~hhyotyni/HH2/HH2.ps
The perceptron-type neurons and networks are typically adapted using
iterative methods. An input that has negligible effect on the output,
still has a non-zero weight, meaning that the corresponding nodes need
to be connected. The resulting network structure is fully connected.
However, there often exist structural dependencies between specific
inputs and outputs, and these dependencies should be utilized to find a
structurally better motivated connections.
For example, `learning a concept', as presented in [2], can be
interpreted as successive application of one layer perceptrons. At
least in this application, `qualitative' rather than `quantitative'
perceptron weight optimization methods are needed---otherwise, the
classification results become more or less `blurred'.
As an alternative to traditional optimization methods, Genetic
Algorithms (GA) have been proposed (for example, see [3]).
This approach makes it possible to optimize the network structure,
because no continuity properties are required. However, GA's are very
inefficient, and the optimality of the result cannot be proven.
It turns out that when the problem setting is written in an appropriate
form, an optimization algorithm for finding a pruned network structure
can be formulated that solves both of the above problems: the
algorithm is fast and its convergence can be proven.
Even if the discussion of perceptron networks with non-differentiable
nonlinearities is not regarded as mainstream neural networks research,
it may be useful to see how simply some difficult-looking things
actually can be done when the problems are studied closer.
Assume that, given inputs 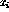 ,
, 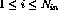 , the outputs
should be
, the outputs
should be 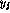 ,
, 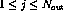 . If the output values are
binary, this task can be called classification. Perceptron networks are
traditionally used for this kind of classification tasks. The
input--output function of a perceptron number j can be characterized as
. If the output values are
binary, this task can be called classification. Perceptron networks are
traditionally used for this kind of classification tasks. The
input--output function of a perceptron number j can be characterized as

where 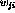 are the weight parameters and
are the weight parameters and 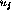 denotes the bias
(see Fig. 1). The activation function
denotes the bias
(see Fig. 1). The activation function 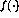 determines the actual output value of the perceptron. Defining a
vector-valued function
determines the actual output value of the perceptron. Defining a
vector-valued function 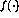 , behaving elementwise as the
previous scalar function, and introducing the
, behaving elementwise as the
previous scalar function, and introducing the 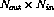 weight matrix W and the
weight matrix W and the 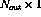 bias vector U, the
operation of a set of
bias vector U, the
operation of a set of 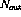 perceptrons can be expressed in a
matrix form as
perceptrons can be expressed in a
matrix form as

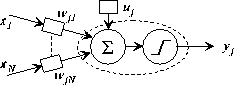
Figure 1: The model for the perceptron number j
Assume that a parameter vector  should be found so that a linear cost
criterion would be optimized, subject to linear constraints:
should be found so that a linear cost
criterion would be optimized, subject to linear constraints:
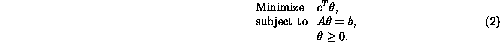
The above problem can be solved by applying the so called Simplex
algorithm (for example, see [4]). It can be shown that this
algorithm always terminates after a finite number of steps, and
usually the operation of the algorithm is very efficient. Systems with
thousands of variables are commonplace.
The linear constraints in (2) are hyperplanes in a
high-dimensional space, together defining a `hyperhedron'. The
operation of the algorithm can be described as a process where one
traverses from a vertex to another until the minimum of the objective
function is reached. In practice, it often turns out that variables
are only utilized if their introduction is unavoidable. This property
of the algorithm facilitates different kinds of structural
optimization schemes.
Next it is shown how the perceptron network optimization problem can
be converted into this linear programming framework.
First, assume that the perceptron is linear, that means, 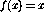 . If
the correct classification at time t is
. If
the correct classification at time t is 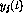 , given inputs
, given inputs
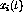 , where
, where 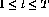 , one can construct constraint
equations for each j,t pair as follows:
, one can construct constraint
equations for each j,t pair as follows:

Because the parameters 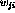 and
and 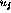 can be positive or negative,
additional variables need to be introduced to match the non-negativity
restriction of (2): the parameters are now expressed as
can be positive or negative,
additional variables need to be introduced to match the non-negativity
restriction of (2): the parameters are now expressed as
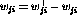 and
and 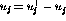 , so that
, so that
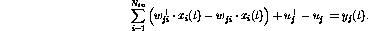
The above set of constraints is valid if the operation of the perceptron is
linear. Now assume that the nonlinearity in the nodes is defined as saturation
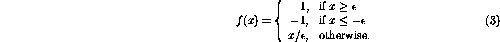
The limit values could be 1 and 0 just as well, without essentially
changing the following derivations.
If the value of 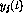 should be on the upper limit, the
corresponding constraint is modified as
should be on the upper limit, the
corresponding constraint is modified as
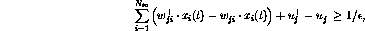
and if 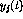 should be on the lower limit,
should be on the lower limit,
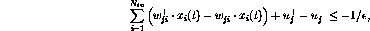
or
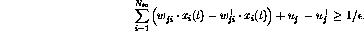
If the network is to be applied to classification tasks, only the two
extreme values for 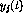 are possible. If the intermediate values are also
possible, the Simplex problem can again be formulated (see [2]).
are possible. If the intermediate values are also
possible, the Simplex problem can again be formulated (see [2]).
Introducing the `slack variables' 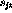 and
and 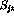 ,
the constraint equations become
,
the constraint equations become
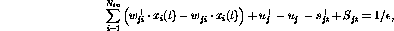
and
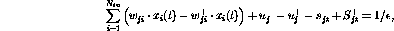
respectively. The reason to introduce the variables 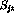 is to
facilitate the `big M' technique in optimization---if these variables
are emphasized in the cost criterion, the search for the feasible
solution can be combined with the optimization.
is to
facilitate the `big M' technique in optimization---if these variables
are emphasized in the cost criterion, the search for the feasible
solution can be combined with the optimization.
In addition to weighting the variables 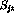 in the optimality
criterion, the parameters
in the optimality
criterion, the parameters 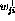 and
and 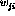 as well as
as well as 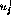 and
and 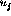 also need to be weighted. This means that there will be two
simultaneous optimization processes going on: first, the classification
error is eliminated, and, second, the sum of the absolute values of the
parameters is minimized. The latter objective means that the network
realizing the input-output mapping will be as simple as possible.
also need to be weighted. This means that there will be two
simultaneous optimization processes going on: first, the classification
error is eliminated, and, second, the sum of the absolute values of the
parameters is minimized. The latter objective means that the network
realizing the input-output mapping will be as simple as possible.
There will be 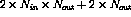 variables and
variables and 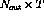 constraint equations in the data
structures defining the optimization problem. Even if the matrices
may become very large, the linear programming problem can still be
solved efficiently.
constraint equations in the data
structures defining the optimization problem. Even if the matrices
may become very large, the linear programming problem can still be
solved efficiently.
Assume that the logical AND operation between the inputs 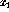 and
and
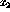 should be realized using a single perceptron. Now,
should be realized using a single perceptron. Now, 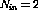 ,
,
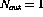 , and T=4. The input patterns are
, and T=4. The input patterns are
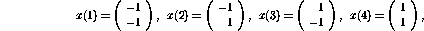
and the corresponding scalar outputs should be
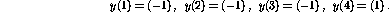
The parameters to be optimized are collected in the vector  :
:
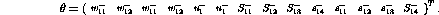
Matrices A and b are presented in the form 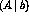 ,
also showing (using `*' symbols) the basis variables
corresponding to each row:
,
also showing (using `*' symbols) the basis variables
corresponding to each row:
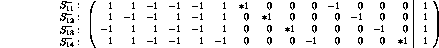
In the b vector, one has now 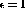 .
The original weighting of the variables, as motivated above, is
.
The original weighting of the variables, as motivated above, is
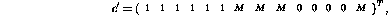
where M is a large number. However, this original set of
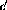 , A, and b does not constitute a feasible solution for the
problem---the basis variables
, A, and b does not constitute a feasible solution for the
problem---the basis variables 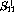 ,
, 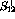 ,
, 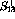 , and
, and
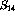 must have zero weights in c. Using the constraint
equations, the objective function can be modified:
must have zero weights in c. Using the constraint
equations, the objective function can be modified:
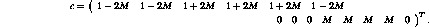
When the Simplex algorithm is applied (for example, see [4]),
the optimum is found after only 4 iterations:
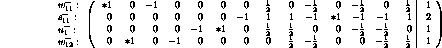
The matrices W and U can directly be constructed from the result.
The basis variables 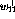 ,
, 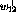 ,
, 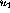 , and
, and 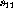 are
the only non-zero variables in the optimal realization, and their values
can directly be seen in the vector b:
are
the only non-zero variables in the optimal realization, and their values
can directly be seen in the vector b:
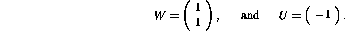
The variable value 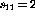 reveals that when the input is
reveals that when the input is
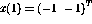 , the node output is
`truncated' from -3 to -1 because of the nonlinearity.
, the node output is
`truncated' from -3 to -1 because of the nonlinearity.
A one-layer perceptron network can only be used for classification if
the classes are linearly separable. Two or more layers of perceptrons
can be used in more complex cases, but because of the non-differentiable
nonlinearities, no efficient adaptation algorithms exist.
One approach to adapting a two-layer perceptron is to randomly select
the first layer weights, and hope that among the hidden layer units,
linearly separable combinations of the inputs emerge---the second layer
can then be adapted using the standard techniques (for example, see
[1]).
This way, however, the number of hidden layer units tends to become large.
The above structural optimization method can be used to `prune'
the network. If a non-optimal two-layer perceptron network exists, the
hidden layer units can be regarded as inputs to the latter part of the
network. After the weights between the hidden layer and the output
layer are optimized, hidden layer units with no connections can be
eliminated. In the second phase, the weights between the inputs and the
remaining hidden units are optimized.
Assume that the goal is to optimize a two-layer perceptron classifier.
The calculation of the hidden layer units z, and, further, the output
layer y, can be presented in the matrix form as

The optimization is carried out in two steps as presented in the previous
section, and only an example is presented here.
The four inputs of dimension two are supposed to be
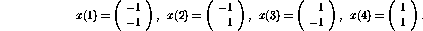
The outputs, corresponding to the above inputs, should be
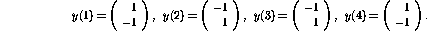
The output 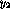 corresponds to the `exclusive or' ( XOR) function of
the two inputs
corresponds to the `exclusive or' ( XOR) function of
the two inputs 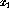 and
and 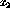 , and
, and 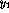 is its negation.
is its negation.
Assume that a two-layer perceptron network with ten hidden layer units
has been created for this classification task using some traditional technique.
The hidden layer values corresponding to the given four inputs are
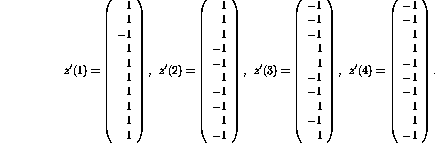
Because the given non-optimal network can perform the classification task,
there must exist linearly separable combinations in
the hidden layer. It is also possible to construct the desired outputs
by applying the one-layer perceptron network between the hidden layer
and the output layer.
The Simplex algorithm is applied (with 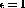 in (3)).
First, the weights between the hidden layer and the output layer are
optimized. All
in (3)).
First, the weights between the hidden layer and the output layer are
optimized. All 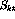 variables have value zero in the optimum---this
means that the desired output mapping can exactly be obtained.
variables have value zero in the optimum---this
means that the desired output mapping can exactly be obtained.
It turns out that only two columns (columns 8 and 9) in the resulting
weight matrix 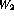 have non-zero elements, so that all other hidden
layer elements except numbers 8 and 9 can be eliminated. The weight
matrices are
have non-zero elements, so that all other hidden
layer elements except numbers 8 and 9 can be eliminated. The weight
matrices are
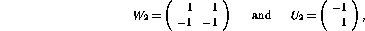
and the two values of the `pruned' hidden layer are
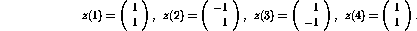
When the 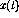 values and the necessary
values and the necessary 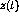 values are known, the
first layer can also be optimized. The result is
values are known, the
first layer can also be optimized. The result is
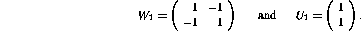
It needs to be noted that this two-phase technique for optimizing a two
layer perceptron network---even if linearly separable hidden layer
values were given---does not necessarily result in an optimal network.
For example, the following realization with three hidden layer
units (but with the same number of links between nodes) gives exactly
the same minimum cost in the second layer optimization phase:
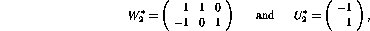
even if the first layer now becomes considerably more complex:
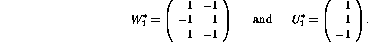
It is also possible to define the perceptron network structure so that
there are recurrent loops:
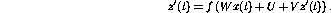
The links between perceptrons are here presented as elements of the
matrix V. Defining 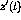 appropriately, any kinds of perceptron
structures can be presented in the same framework---for example, it is
not necessary to distinguish between the `hidden layer' nodes and the
`output' nodes, and the vector can be constructed as
appropriately, any kinds of perceptron
structures can be presented in the same framework---for example, it is
not necessary to distinguish between the `hidden layer' nodes and the
`output' nodes, and the vector can be constructed as

The above formulation can again be written in the linear programming
form---first, assuming that 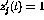 , one has
, one has
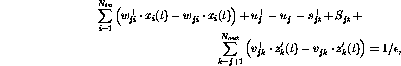
and if 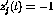 ,
,
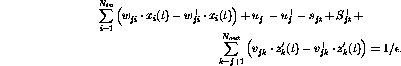
For optimization purposes, a set of feasible 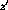 values are again
needed---only after that the optimization between them becomes possible.
In the following example, the solution that was found in the previous
section, is used as the starting point for finding an optimized solution
for the same XOR problem:
values are again
needed---only after that the optimization between them becomes possible.
In the following example, the solution that was found in the previous
section, is used as the starting point for finding an optimized solution
for the same XOR problem:
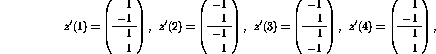
with the input values  as given in the previous section.
It turns out that the resulting matrices are
as given in the previous section.
It turns out that the resulting matrices are
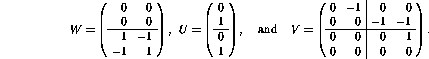
The structure of the matrix V was restricted in the equations to be
upper triangular with zero diagonal elements. This rather heuristic
limitation may result in suboptimal solutions. However, recurrent
structures cause severe difficulties---for example, allowing diagonal
elements in V, any 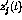 value could trivially be explained
using only the node itself!
value could trivially be explained
using only the node itself!
The `upper triangular' construction of V allows the output nodes 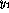 and
and 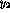 to be explained not only in terms of all of the hidden nodes and the
inputs, but the output nodes can also be linked---this possibility makes
the optimized structure simpler than would have been possible using
strict node level hierarchy (see Fig. 2).
to be explained not only in terms of all of the hidden nodes and the
inputs, but the output nodes can also be linked---this possibility makes
the optimized structure simpler than would have been possible using
strict node level hierarchy (see Fig. 2).
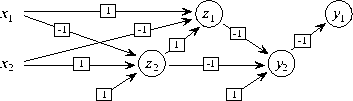
Figure 2: An optimized multi-level realization
This research has been financed by the Academy of Finland, and this
support is gratefully acknowledged.
References
- 1
-
Demuth, H. and Beale, M.:
Neural Network Toolbox User's Guide.
MathWorks, Inc., Natick, Massachusetts,
1994.
- 2
-
Hyötyniemi, H.:
Correlations---Building Blocks of Intelligence?
In Älyn ulottuvuudet ja oppihistoria (History and dimensions
of intelligence), Finnish Artificial Intelligence
Society, 1995, pp. 199--226.
- 3
-
Nissinen, A.:
Structural Optimization of Feedforward Neural Networks using Genetic
Algorithm.
Tampere University of Technology, Control Engineering Laboratory,
Report 5, 1994.
- 4
-
Taha, H.A.:
Operations Research---An Introduction.
MacMillan Publishing, New York, 1992 (5th edition).
Structural Optimization of Feedforward Networks
This document was generated using the LaTeX2HTML translator Version 95.1 (Fri Jan 20 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -show_section_numbers HH2.tex.
The translation was initiated by Heikki Hy|tyniemi on Mon Aug 26 12:50:30 EET DST 1996
- ...Networks
-
This paper was presented at the Symposium on Artificial Networks
(Finnish Artificial Intelligence Conference), August 19--23, in Vaasa,
Finland, organized by the Finnish Artificial Intelligence Society and
University of Vaasa. Published in "STeP'96---Genes, Nets and
Symbols", edited by Alander, J., Honkela, T., and Jakobsson, M.,
Finnish Artificial Intelligence Society,
pp. 25--34.
Heikki Hy|tyniemi
Mon Aug 26 12:50:30 EET DST 1996
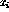 ,
, 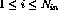 , the outputs
should be
, the outputs
should be 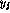 ,
, 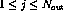 . If the output values are
binary, this task can be called classification. Perceptron networks are
traditionally used for this kind of classification tasks. The
input--output function of a perceptron number j can be characterized as
. If the output values are
binary, this task can be called classification. Perceptron networks are
traditionally used for this kind of classification tasks. The
input--output function of a perceptron number j can be characterized as

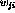 are the weight parameters and
are the weight parameters and 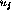 denotes the bias
(see Fig.
denotes the bias
(see Fig. 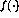 determines the actual output value of the perceptron. Defining a
vector-valued function
determines the actual output value of the perceptron. Defining a
vector-valued function 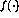 , behaving elementwise as the
previous scalar function, and introducing the
, behaving elementwise as the
previous scalar function, and introducing the 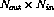 weight matrix W and the
weight matrix W and the 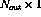 bias vector U, the
operation of a set of
bias vector U, the
operation of a set of 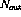 perceptrons can be expressed in a
matrix form as
perceptrons can be expressed in a
matrix form as


 should be found so that a linear cost
criterion would be optimized, subject to linear constraints:
should be found so that a linear cost
criterion would be optimized, subject to linear constraints:
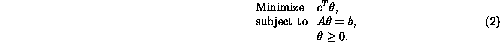
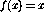 . If
the correct classification at time t is
. If
the correct classification at time t is 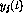 , given inputs
, given inputs
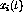 , where
, where 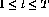 , one can construct constraint
equations for each j,t pair as follows:
, one can construct constraint
equations for each j,t pair as follows:

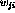 and
and 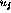 can be positive or negative,
additional variables need to be introduced to match the non-negativity
restriction of (
can be positive or negative,
additional variables need to be introduced to match the non-negativity
restriction of (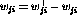 and
and 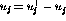 , so that
, so that
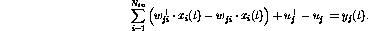
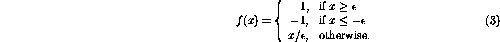
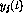 should be on the upper limit, the
corresponding constraint is modified as
should be on the upper limit, the
corresponding constraint is modified as
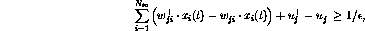
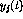 should be on the lower limit,
should be on the lower limit,
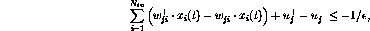
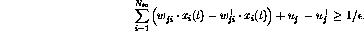
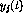 are possible. If the intermediate values are also
possible, the Simplex problem can again be formulated (see [
are possible. If the intermediate values are also
possible, the Simplex problem can again be formulated (see [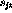 and
and 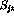 ,
the constraint equations become
,
the constraint equations become
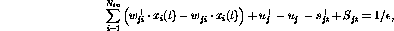
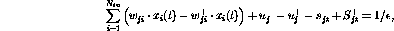
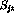 is to
facilitate the `big M' technique in optimization---if these variables
are emphasized in the cost criterion, the search for the feasible
solution can be combined with the optimization.
is to
facilitate the `big M' technique in optimization---if these variables
are emphasized in the cost criterion, the search for the feasible
solution can be combined with the optimization.
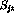 in the optimality
criterion, the parameters
in the optimality
criterion, the parameters 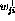 and
and 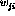 as well as
as well as 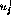 and
and 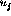 also need to be weighted. This means that there will be two
simultaneous optimization processes going on: first, the classification
error is eliminated, and, second, the sum of the absolute values of the
parameters is minimized. The latter objective means that the network
realizing the input-output mapping will be as simple as possible.
also need to be weighted. This means that there will be two
simultaneous optimization processes going on: first, the classification
error is eliminated, and, second, the sum of the absolute values of the
parameters is minimized. The latter objective means that the network
realizing the input-output mapping will be as simple as possible.
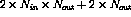 variables and
variables and 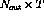 constraint equations in the data
structures defining the optimization problem. Even if the matrices
may become very large, the linear programming problem can still be
solved efficiently.
constraint equations in the data
structures defining the optimization problem. Even if the matrices
may become very large, the linear programming problem can still be
solved efficiently.
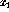 and
and
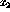 should be realized using a single perceptron. Now,
should be realized using a single perceptron. Now, 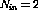 ,
,
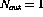 , and T=4. The input patterns are
, and T=4. The input patterns are
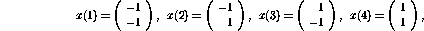
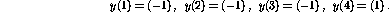
 :
:
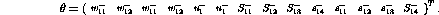
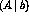 ,
also showing (using `*' symbols) the basis variables
corresponding to each row:
,
also showing (using `*' symbols) the basis variables
corresponding to each row:
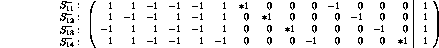
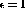 .
The original weighting of the variables, as motivated above, is
.
The original weighting of the variables, as motivated above, is
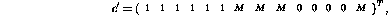
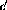 , A, and b does not constitute a feasible solution for the
problem---the basis variables
, A, and b does not constitute a feasible solution for the
problem---the basis variables 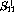 ,
, 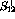 ,
, 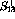 , and
, and
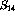 must have zero weights in c. Using the constraint
equations, the objective function can be modified:
must have zero weights in c. Using the constraint
equations, the objective function can be modified:
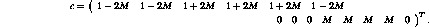
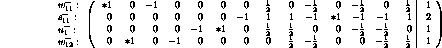
 ,
, 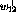 ,
, 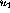 , and
, and 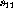 are
the only non-zero variables in the optimal realization, and their values
can directly be seen in the vector b:
are
the only non-zero variables in the optimal realization, and their values
can directly be seen in the vector b:
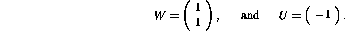
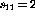 reveals that when the input is
reveals that when the input is
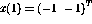 , the node output is
`truncated' from -3 to -1 because of the nonlinearity.
, the node output is
`truncated' from -3 to -1 because of the nonlinearity.

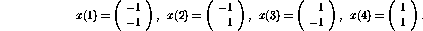
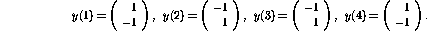
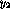 corresponds to the `exclusive or' ( XOR) function of
the two inputs
corresponds to the `exclusive or' ( XOR) function of
the two inputs 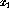 and
and 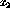 , and
, and 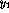 is its negation.
is its negation.
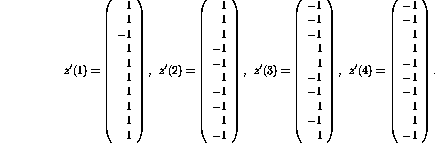
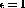 in (
in ( variables have value zero in the optimum---this
means that the desired output mapping can exactly be obtained.
variables have value zero in the optimum---this
means that the desired output mapping can exactly be obtained.
 have non-zero elements, so that all other hidden
layer elements except numbers 8 and 9 can be eliminated. The weight
matrices are
have non-zero elements, so that all other hidden
layer elements except numbers 8 and 9 can be eliminated. The weight
matrices are
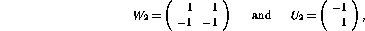
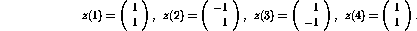
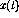 values and the necessary
values and the necessary 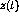 values are known, the
first layer can also be optimized. The result is
values are known, the
first layer can also be optimized. The result is
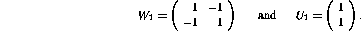
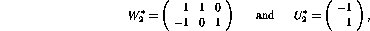
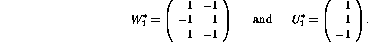
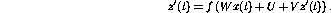
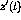 appropriately, any kinds of perceptron
structures can be presented in the same framework---for example, it is
not necessary to distinguish between the `hidden layer' nodes and the
`output' nodes, and the vector can be constructed as
appropriately, any kinds of perceptron
structures can be presented in the same framework---for example, it is
not necessary to distinguish between the `hidden layer' nodes and the
`output' nodes, and the vector can be constructed as

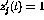 , one has
, one has
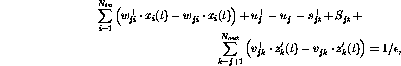
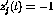 ,
,
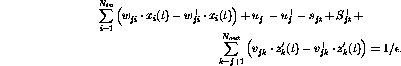
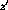 values are again
needed---only after that the optimization between them becomes possible.
In the following example, the solution that was found in the previous
section, is used as the starting point for finding an optimized solution
for the same XOR problem:
values are again
needed---only after that the optimization between them becomes possible.
In the following example, the solution that was found in the previous
section, is used as the starting point for finding an optimized solution
for the same XOR problem:
 as given in the previous section.
It turns out that the resulting matrices are
as given in the previous section.
It turns out that the resulting matrices are
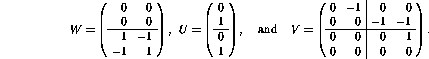
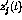 value could trivially be explained
using only the node itself!
value could trivially be explained
using only the node itself!
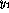 and
and 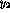 to be explained not only in terms of all of the hidden nodes and the
inputs, but the output nodes can also be linked---this possibility makes
the optimized structure simpler than would have been possible using
strict node level hierarchy (see Fig.
to be explained not only in terms of all of the hidden nodes and the
inputs, but the output nodes can also be linked---this possibility makes
the optimized structure simpler than would have been possible using
strict node level hierarchy (see Fig. 