



Next: Applications
Up: Inductive logic programming
Previous: Example on wine tasting
Contents
The wine tasting example is simple: The data consist of a single table
and each row had only one index (the name of the person). This case is
called attribute-value learning or propositional learning. The case with
relational data in multiple tables and with multiple indices is more complex. In the
wine example, first we need to reformulate
 as
as
 , that is, every person
, that is, every person  who
likes
who
likes  , also likes
, also likes  . Then, we could also have knowledge of
marriages between people, that is,
. Then, we could also have knowledge of
marriages between people, that is,
 is true iff
is true iff  is the husband of
is the husband of  .
Now the hypotheses include clauses such as
.
Now the hypotheses include clauses such as
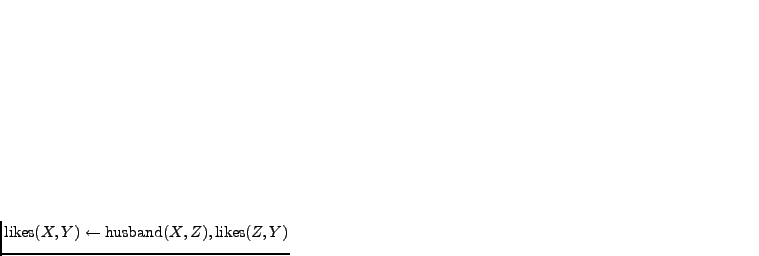 , that is, every husband
, that is, every husband  likes all the
wines
likes all the
wines  that his wife
that his wife  likes. We could also know the grape and
origin of each wine and make a hypothesis that anyone who likes a wine
that is made of Pinot Noir likes all wines from the same origin. The
hypothesis space becomes more complex, but the trellis
defined by the generality relationships is still present as is.
likes. We could also know the grape and
origin of each wine and make a hypothesis that anyone who likes a wine
that is made of Pinot Noir likes all wines from the same origin. The
hypothesis space becomes more complex, but the trellis
defined by the generality relationships is still present as is.
For traversing the hypothesis space, refinement operators are
used. One is the most general specialisation,
 , that
corresponds to an edge downwards in the lattice of
Figure 5.1. Let us define that
, that
corresponds to an edge downwards in the lattice of
Figure 5.1. Let us define that  means that
means that  is
more specific than
is
more specific than  . Hypothesis
. Hypothesis
 iff
iff  and there
is no hypothesis
and there
is no hypothesis  such that
such that  . For example, hypothesis
. For example, hypothesis
 is more specific than hypothesis
is more specific than hypothesis  since everyone who
likes both wines
since everyone who
likes both wines  and
and  trivially like wine
trivially like wine  . The hypothesis
. The hypothesis  is
also a most general specialisation of
is
also a most general specialisation of  since there is no other
hypothesis that would fit between these two. Note that a hypothesis
may have more than one most general specialisation. The least
general generalisation,
since there is no other
hypothesis that would fit between these two. Note that a hypothesis
may have more than one most general specialisation. The least
general generalisation,
 , is the inverse of
, is the inverse of
 . It
corresponds to an edge upwards in the hypothesis lattice.
. It
corresponds to an edge upwards in the hypothesis lattice.
 iff
iff  and there is no
and there is no  such that
such that  .
.
One can generate all (possibly infinite) hypotheses in the hypothesis space
if one applies the most general specialisation operation to the null
hypothesis repeatedly. Two of such systems include FOIL
by Quinlan (1990) and PROGOL by Muggleton (1995). Some ILP systems, such
as GOLEM by Muggleton and Feng (1992) and Aleph by Srinivasan (2005), start from
the most specific hypotheses and work their way upwards using the
least general generalisation, and some ILP systems use both types of
refinement operators. There are dozens of ILP systems listed on the
web page5.2 of Network
of Excellence in Inductive Logic Programming ILPnet2.




Next: Applications
Up: Inductive logic programming
Previous: Example on wine tasting
Contents
Tapani Raiko
2006-11-21
 as
as
 , that is, every person
, that is, every person  who
likes
who
likes  , also likes
, also likes  . Then, we could also have knowledge of
marriages between people, that is,
. Then, we could also have knowledge of
marriages between people, that is,
 is true iff
is true iff  is the husband of
is the husband of  .
Now the hypotheses include clauses such as
.
Now the hypotheses include clauses such as
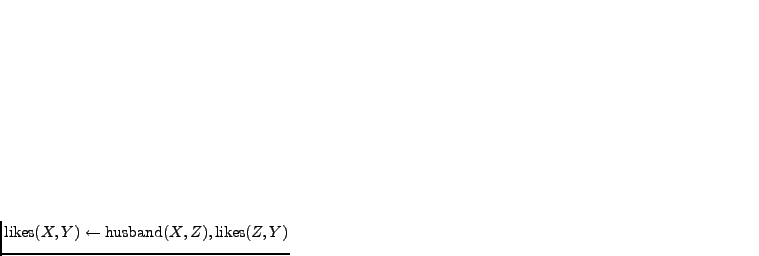 , that is, every husband
, that is, every husband  likes all the
wines
likes all the
wines  that his wife
that his wife  likes. We could also know the grape and
origin of each wine and make a hypothesis that anyone who likes a wine
that is made of Pinot Noir likes all wines from the same origin. The
hypothesis space becomes more complex, but the trellis
defined by the generality relationships is still present as is.
likes. We could also know the grape and
origin of each wine and make a hypothesis that anyone who likes a wine
that is made of Pinot Noir likes all wines from the same origin. The
hypothesis space becomes more complex, but the trellis
defined by the generality relationships is still present as is.
 , that
corresponds to an edge downwards in the lattice of
Figure
, that
corresponds to an edge downwards in the lattice of
Figure  means that
means that  is
more specific than
is
more specific than  . Hypothesis
. Hypothesis
 iff
iff  such that
such that  . For example, hypothesis
. For example, hypothesis
 is more specific than hypothesis
is more specific than hypothesis  since everyone who
likes both wines
since everyone who
likes both wines  , is the inverse of
, is the inverse of
 iff
iff  and there is no
and there is no  .
.