![]()
Kynnyspiiri (engl. threshold circuit, multilayer perceptron)
on kombinaatiopiiri, jonka portteina voi olla mielivaltaisia kynnysfunktioita
![]() ,
, ![]() .
Todista seuraavat tulokset:
.
Todista seuraavat tulokset:
-
Jos syötteinä on käytettävissä sekä muuttujat
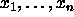 että niiden negaatiot
että niiden negaatiot 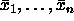 , niin mikä
tahansa muuttujien
, niin mikä
tahansa muuttujien 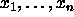 monomi (literaalien konjunktio)
voidaan laskea yhdellä kynnysportilla
monomi (literaalien konjunktio)
voidaan laskea yhdellä kynnysportilla 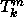 ,
, 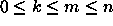 .
. -
Mikä tahansa n muuttujan Boolen funktio f voidaan laskea
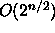 -porttisella kynnyspiirillä.
(Vihje: Laske ensin kaikki muuttujien
-porttisella kynnyspiirillä.
(Vihje: Laske ensin kaikki muuttujien
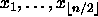 monomit. Tarkastele sitten
funktion f dnf-esitystä ja eri monomien esiintymistä siinä.)
monomit. Tarkastele sitten
funktion f dnf-esitystä ja eri monomien esiintymistä siinä.) -
Melkein kaikkien n muuttujan Boolen funktioiden laskeminen
kynnyspiireillä vaatii
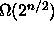 porttia.
(Vrt. Shannonin lause;
täsmennä itse, mitä ``melkein kaikki'' tarkoittaa tässä yhteydessä.)
porttia.
(Vrt. Shannonin lause;
täsmennä itse, mitä ``melkein kaikki'' tarkoittaa tässä yhteydessä.)
![]()
KÄÄNNÄ
Näillä merkinnöillä on siis ![]() ja
ja
![]() .
Merkitään edelleen
.
Merkitään edelleen ![]() .
Todista seuraavat luokkien MIP ja
.
Todista seuraavat luokkien MIP ja
![]() suhdetta koskevat väitteet:
suhdetta koskevat väitteet:
-
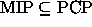 . (Ohje:
Oraakkelien määrän lisäksi MIP- ja PCP-systeemeillä
on se ero, että MIP-oraakkelit voivat ``muistaa'' aiemmat
vastauksensa ja mukauttaa myöhemmän toimintansa niiden mukaan,
kun taas PCP-oraakkelin vastaukset on kiinnitetty ennalta.
Tämän tehtävän ideana on siis suunnitella koodaus, jolla k
adaptiivisen oraakkelin kysymys/vastausjonot voidaan koodata
yhteen kiinteään oraakkeliin.)
. (Ohje:
Oraakkelien määrän lisäksi MIP- ja PCP-systeemeillä
on se ero, että MIP-oraakkelit voivat ``muistaa'' aiemmat
vastauksensa ja mukauttaa myöhemmän toimintansa niiden mukaan,
kun taas PCP-oraakkelin vastaukset on kiinnitetty ennalta.
Tämän tehtävän ideana on siis suunnitella koodaus, jolla k
adaptiivisen oraakkelin kysymys/vastausjonot voidaan koodata
yhteen kiinteään oraakkeliin.) -
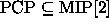 . (Vihje: Käytä toista
MIP-oraakkelia PCP-oraakkelin koodaukseen ja toista
oraakkelia sen varmistamiseen, että ensimmäinen oraakkeli
ei muuttele vastauksiaan.)
. (Vihje: Käytä toista
MIP-oraakkelia PCP-oraakkelin koodaukseen ja toista
oraakkelia sen varmistamiseen, että ensimmäinen oraakkeli
ei muuttele vastauksiaan.)
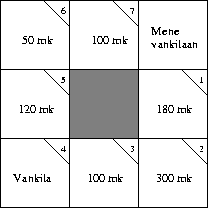
Peliä pelataan noppien sijaan rahaa heittämällä siten, että kun rahanheiton tulos on ``kruuna'', pelaaja siirtyy yhden ruudun eteenpäin, ja kun tulos on klaava, hän siirtyy kaksi ruutua eteenpäin. Mallinna peli Markovin ketjuna ja määritä pelaajan eri ruuduille sijoittumistodennäköisyyksien tasapainojakauma äärettömän pitkässä pelissä. Määritä tämän jakauman ja lautaan merkittyjen eri ruutujen ``vuokrien'' perusteella, mikä on laudan paras ruutu (so. se, josta vastapelaaja pitkän ajan kuluessa joutuu odotusarvoisesti maksamaan eniten vuokraa).