Tietojenkäsittelyteoria, kevät 2000
Harjoitus 6, to 2.3. klo 10-12 sali MaD381

1. Miksi luentojen lauseen 4.10 (`` '') todistus edellyttää, että simuloitava kone on deterministinen (eikä esim. epädeterministinen)?
2. Alternoiva Turingin kone on -kone ( -kone), , jos sen alkutila on eksistentiaalinen (universaalinen), ja missä tahansa koneen laskennassa (so. millä tahansa laskentapolulla) koneen tila vaihtuu eksistentiaalisesta universaaliseksi tai toisinpäin (kone ``alternoi'') enintään k-1 kertaa. Lisäksi voidaan deterministisiä koneita sanoa - tai -koneiksi. Määritellään vaativuusluokat:

   

   Osoita, että kaikilla on ja . (Ohje: Todistus induktiolla k:n suhteen. Induktioaskelta varten tarkastele mielivaltaisen polynomisessa ajassa toimivan -koneen M tunnistamaa kieltä A, ja sen rinnalla kieltä

   

   Totea, että kieli kuuluu luokkaan , ja että väite seuraa tästä pienillä lisätarkasteluilla. Huom.: Vastaavalla argumentilla voidaan osoittaa, että Savitchin lauseen seurauksena on

   

   kaikilla .)

3. Osoita, että kaikilla seuraava kieli on -täydellinen:

   

   Huomautus: Myös kieltä QBF rajoittamalla saadaan luonnollisia -täydellisiä kieliä:

   

   (Todistus saadaan tässä tapauksessa yksinkertaisesti soveltamalla Cookin lauseen todistusta epädeterminististen koneiden sijaan alternoiviin Turingin koneisiin.)

   Kurssin ensimmäinen välikoe on ke 1.3. klo 8-11. Kokeen alue on kurssin alusta alternoiviin Turingin koneisiin asti.

   KÄÄNNÄ

4. Olkoon A on jokin rekursiivinen kieli ja jokin rekursiivisesti esitettävä rekursiivisten kielten luokka, joka on suljettu äärellisten variaatioiden suhteen. Voidaan todeta (ei tarvitse todistaa), että tällöin seuraavat kieliluokat ovat rekursiivisesti esitettäviä:
   1. ;
   2. .

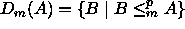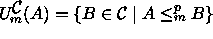   Todista tätä tietoa ja luentojen Lausetta 5.5 (uniformi diagonalisointilause) käyttäen seuraavat väitteet kaikilla :

   1. Jos 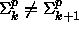, niin luokka 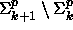sisältää kieliä, jotka eivät ole 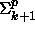-täydellisiä.
   2. Jos 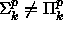, niin luokka 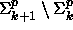sisältää kieliä, jotka eivät ole 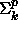-kovia eivätkä 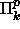-kovia (so. joihin ei voi 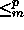-palauttaa tehtävän 3 kieltä 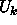eikä kieltä ).
5. Todista, edellisen tehtävän tapaan, seuraava rekursiivisten kielten -järjestystä koskeva tiheystulos. Olkoot ja rekursiivisia kieliä, joilla (so. , mutta ). Tällöin on olemassa rekursiivinen kieli A, jolla .

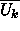   Lisätieto: Samaa tekniikkaa käyttäen voidaan itse asiassa todistaa seuraava vahvempikin tulos. Jos ja ovat rekursiivisia kieliä, joilla , niin on olemassa rekursiiviset kielet , joilla

   1. kaikilla i on ;
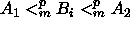   2. kaikilla 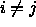on 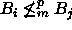, 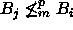(so. kielet 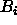ja 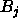ovat pareittain vertautumattomia).

Kurssin ensimmäinen välikoe on ke 1.3. klo 8-11. Kokeen alue on kurssin alusta alternoiviin Turingin koneisiin asti.