


Next: About this document ...
Up: prob9
Previous: prob9
- Determine the capacity of the binary symmetric channel BSC(
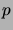 ),
when (a)
),
when (a) 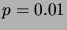 , (b)
, (b) 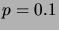 , (c)
, (c) 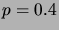 .
.
- Show that the Hamming distance
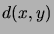 between
between 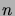 -bit binary
strings is a metric in the space
-bit binary
strings is a metric in the space 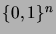 , i.e. for all
, i.e. for all
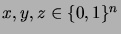 the following hold:
the following hold:
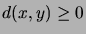 ,
,
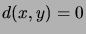 if and only if
if and only if 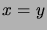 ,
,
-
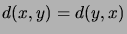 ,
,
-
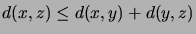 (``triangle inequality'').
(``triangle inequality'').
(Of course only condition (d) is nontrivial in this case.)
- List all the codewords of the Hamming code
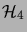 (4 data bits, 3 parity bits,
single-error correction), when the parity check matrix
(4 data bits, 3 parity bits,
single-error correction), when the parity check matrix
 is given in standard form. (``Standard form'' = the identity
matrix
is given in standard form. (``Standard form'' = the identity
matrix 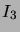 corresponding to the parity bits is located in the
rightmost columns of the check matrix
corresponding to the parity bits is located in the
rightmost columns of the check matrix 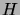 .)
.)
- Prove that a single-error correcting 7-bit code can have
at most 16 codewords, and hence the code
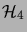 has maximal rate within this class of codes.
has maximal rate within this class of codes.
- Design a single-error correcting 5-bit binary code with 4 codewords.
Is the rate of this code higher or lower than that of the Hamming code
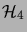 ?
?
- Mr.
 and Ms.
and Ms. 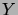 are enjoying a pleasant evening in a somewhat
noisy restaurant, whose noise level is modeled by the channel
BSC(0.1). Mr.
are enjoying a pleasant evening in a somewhat
noisy restaurant, whose noise level is modeled by the channel
BSC(0.1). Mr. 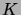 would like to send Ms.
would like to send Ms. 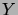 the 4-bit message
``0101''.
the 4-bit message
``0101''.
- What is the probability that the message is received correctly,
if Mr.
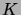 doesn't code it in any way?
doesn't code it in any way?
- How does the situation change if Mr.
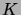 repeats the message
three times, and Ms.
repeats the message
three times, and Ms. 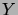 chooses as the value of each bit that
which occurred in the majority of repetitions?
(I.e., in this case two times out of three.)
chooses as the value of each bit that
which occurred in the majority of repetitions?
(I.e., in this case two times out of three.)
- How about if Mr.
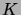 codes the message using the Hamming code
codes the message using the Hamming code
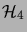 ? What is the coded form of the message in this case?
? What is the coded form of the message in this case?
- Decode the bitstring 1001010, which corresponds to a codeword
of the natural
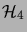 code with a one-bit error.
(``Natural'' = the columns of the parity check matrix
code with a one-bit error.
(``Natural'' = the columns of the parity check matrix 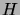 ,
when interpreted as binary numbers, are in numerically
increasing orded.)
What are the contents of the 4 ``message bits'' in the
correct 7-bit codeword.
,
when interpreted as binary numbers, are in numerically
increasing orded.)
What are the contents of the 4 ``message bits'' in the
correct 7-bit codeword.
The second Midterm Exam of the course takes place
Wed 29 November at 8-11 a.m. The exam covers the material
discussed in Problem Sets 6 thru 9 (graphs and coding).



Next: About this document ...
Up: prob9
Previous: prob9
Pekka Orponen
2000-11-16
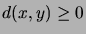 ,
,
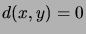 if and only if
if and only if 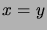 ,
,
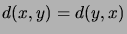 ,
,
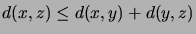 (``triangle inequality'').
(``triangle inequality'').
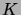 doesn't code it in any way?
doesn't code it in any way?
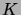 repeats the message
three times, and Ms.
repeats the message
three times, and Ms. 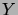 chooses as the value of each bit that
which occurred in the majority of repetitions?
(I.e., in this case two times out of three.)
chooses as the value of each bit that
which occurred in the majority of repetitions?
(I.e., in this case two times out of three.)
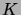 codes the message using the Hamming code
codes the message using the Hamming code
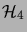 ? What is the coded form of the message in this case?
? What is the coded form of the message in this case?