Next: About this document ...
Up: prob6
Previous: prob6
- Draw a picture of the complete bipartite graph
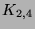 and write down its adjacency matrix. Describe in general
terms the adjacency matrices of graphs
and write down its adjacency matrix. Describe in general
terms the adjacency matrices of graphs 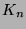 ,
,
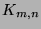 and
and 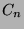 .
.
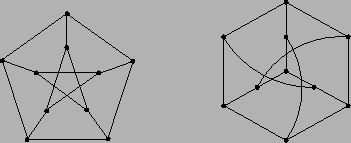
- Prove that the two graphs in the following picture are isomorphic.
(The picture shows two layouts of the Petersen graph,
which is an often encountered example or counterexample in
many graph-theoretic constructions.)
- Draw pictures of all the non-isomorphic 4-vertex (undirected, simple)
graphs. How long would it approximately take to enumerate
all the 15-vertex graphs on a computer capable of enumerating one
graph per nanosecond?
- Prove that if an apartment has only one door out, then at least
one of its rooms must have an odd number of doors.
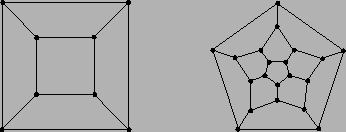
- It was observed by Sir William Rowan Hamilton in 1856
that every graph generated by the vertices and edges of
a regular solid contains a Hamiltonian cycle. Verify his
observation for the following graphs that correspond to
the cube and the regular dodecahedron (regular 12-sided
solid).
- Let
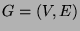 be an (undirected) graph, all of whose vertices
are of even degree. Prove that the edges of
be an (undirected) graph, all of whose vertices
are of even degree. Prove that the edges of  can be oriented
so that in the resulting directed graph the in- and outdegrees
of each vertex (i.e. the number of incoming and outgoing arcs
at that vertex) are equal.
can be oriented
so that in the resulting directed graph the in- and outdegrees
of each vertex (i.e. the number of incoming and outgoing arcs
at that vertex) are equal.
- A piece in the game of dominoes has the shape of a rectangle
divided into two squares, each of which contains from zero
to six ``eyes''. If one leaves out the pieces whose sides
contain twice the same number of eyes, and considers the
orientation of a piece inessential, one observes that the
pieces correspond exactly to two-element sets
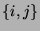 , where
, where
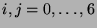 ,
, 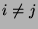 .
Prove that the
.
Prove that the
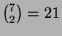 domino pieces thus obtained
can be ordered into a closed ring that respects the rules of
the game, i.e. where the number of eyes in two adjacent
squares are always equal.
As an example, the following picture shows a legal placing
of the pieces
domino pieces thus obtained
can be ordered into a closed ring that respects the rules of
the game, i.e. where the number of eyes in two adjacent
squares are always equal.
As an example, the following picture shows a legal placing
of the pieces 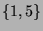 ja
ja 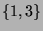 .
(Hint: Consider the graph
.
(Hint: Consider the graph 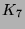 .)
.)



Next: About this document ...
Up: prob6
Previous: prob6
Pekka Orponen
2000-11-09