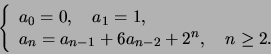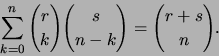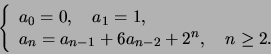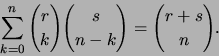Next: About this document ...
Up: prob5
Previous: prob5
- Consider a system of
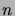 non-parallel lines in the
plane, no three of which intersect at the same point.
(One can think of the lines having been drawn in
sequence so that each ``new'' line intersects all
the ``old'' lines, each at a different point.)
Denote by
non-parallel lines in the
plane, no three of which intersect at the same point.
(One can think of the lines having been drawn in
sequence so that each ``new'' line intersects all
the ``old'' lines, each at a different point.)
Denote by 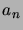 the number of planar subdivisions
thus formed, i.e.
the number of planar subdivisions
thus formed, i.e. 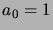 ,
, 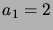 ,
, 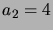 ,
, 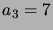 etc.
Find a recurrence equation for the
sequence
etc.
Find a recurrence equation for the
sequence 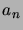 and solve it.
and solve it.
- Solve, using generating functions, the recurrence:
- Establish, using generating functions, the
summation rule for binomial coefficients
known as the Vandermonde convolution:
(Hint:
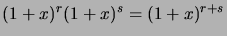 .) Can you
come up with a purely combinatorial proof of the result?
.) Can you
come up with a purely combinatorial proof of the result?
- How many integer solutions does the equation
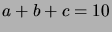 have,
under the constraints that the value of each
variable must be at least 2 and at most 5?
have,
under the constraints that the value of each
variable must be at least 2 and at most 5?
- The Council of the Faculty of Combination Technology
consists of 9 representatives from three groups:
professors, other staff, and students.
In how many ways can the Council be composed so that
each group gets at least one representative, but
no group has an absolute majority on its own?
(Hint: Apply the summation formula
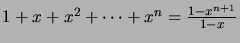 , and
the results of Problem 5 in the previous Problem Set.)
, and
the results of Problem 5 in the previous Problem Set.)
- A box contains 30 blue, 40 red, and 50 green balls.
How many different selections of 70 balls can be made
from its contents?
(Hint: As in the preceding Problem.)
- The cash register line at the University cafeteria has
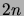 randomly ordered students waiting to pay for their food.
A student lunch costs 10 FIM, and half of the students are
in possession of a 10 FIM coin, while the other half only
have 20 FIM bills. Initially, the cash register of the
cafeteria is empty. What is the probability that the
register can serve all the
randomly ordered students waiting to pay for their food.
A student lunch costs 10 FIM, and half of the students are
in possession of a 10 FIM coin, while the other half only
have 20 FIM bills. Initially, the cash register of the
cafeteria is empty. What is the probability that the
register can serve all the 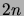 students, without
running out of change at any point?
(Hint: Let
students, without
running out of change at any point?
(Hint: Let 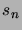 denote the number of those favourable
student lineups, where the cash register contains a
nonnegative amount of money throughout the whole process.
Clearly
denote the number of those favourable
student lineups, where the cash register contains a
nonnegative amount of money throughout the whole process.
Clearly 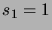 . The value of
. The value of 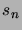 , for
, for 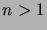 , can
be deduced e.g. by considering after how many student pairs
the amount of money in the register first returns to zero.
If this happens only at the very end, then it must have been
the case that the first student had a 10 FIM coin, the last
student had a 20 FIM bill, and throughout the whole intermediate
interval the register contained a positive amount of money:
there are a total of
, can
be deduced e.g. by considering after how many student pairs
the amount of money in the register first returns to zero.
If this happens only at the very end, then it must have been
the case that the first student had a 10 FIM coin, the last
student had a 20 FIM bill, and throughout the whole intermediate
interval the register contained a positive amount of money:
there are a total of 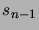 such lineups.
Otherwise there is some smallest number
such lineups.
Otherwise there is some smallest number 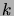 of student pairs,
of student pairs,
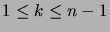 , after which the register returns to zero.
In this case ...
[Note: You need to know about Catalan numbers to
solve this problem.])
, after which the register returns to zero.
In this case ...
[Note: You need to know about Catalan numbers to
solve this problem.])
The first Midterm Exam of the course takes place on Wed 25
October at 8-11 a.m. The exam covers the material discussed
in Problem Sets 1 thru 5.



Next: About this document ...
Up: prob5
Previous: prob5
Pekka Orponen
2000-10-19