Next: About this document ...
Up: prob4
Previous: prob4
- Walking up a staircase, one can ascend either 1 or 2 stairs
at a time. Construct a recurrence relation that describes
how many different ways there are to ascend an
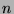 -stair staircase.
(Hint: Partition the ways to ascend an
-stair staircase.
(Hint: Partition the ways to ascend an 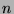 -staircase
according to whether the first step ascends 1 or 2 stairs.)
-staircase
according to whether the first step ascends 1 or 2 stairs.)
- Solve the following recurrences using the
technique of characteristic polynomials:
-
-
- Let
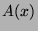 be the generating function for sequence
be the generating function for sequence
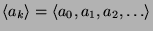 ,
and
,
and
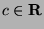 ,
,
 some constants.
Find the sequences corresponding to the following functions:
some constants.
Find the sequences corresponding to the following functions:
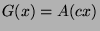 ,
,
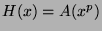 ,
,
-
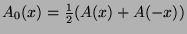 and
and
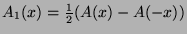 ?
?
- Find the generating functions for the following sequences:
-
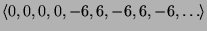 ;
;
-
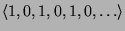 ;
;
-
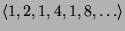 ;
;
-
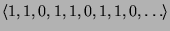 .
.
- Newton's (generalized) binomial theorem states that the following
expansion holds for all values of
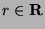 and
and 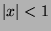 :
:
where the generalized binomial coefficient
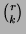 is defined as:
is defined as:
Additionally, one stipulates that
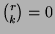 for
for 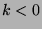 .
Establish the following properties of the generalized binomial
coefficients:
.
Establish the following properties of the generalized binomial
coefficients:
-
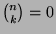 , when
, when
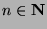 and
and 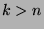 ;
;
-
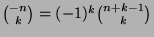 , for
, for
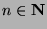 ;
;
-
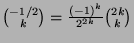 ,
,
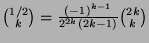 .
.
- Find the sequences corresponding to the functions
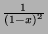 and
and
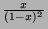 . (Hint: Apply the results of
Problem 5.)
. (Hint: Apply the results of
Problem 5.)
- Solve the recurrence of Problem 2(b) using the technique of
generating functions.



Next: About this document ...
Up: prob4
Previous: prob4
Pekka Orponen
2000-10-16
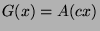 ,
,
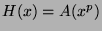 ,
,
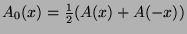 and
and
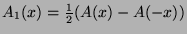 ?
?
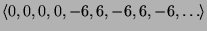 ;
;
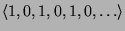 ;
;
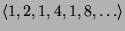 ;
;
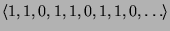 .
.
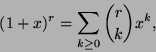
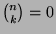 , when
, when
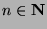 and
and 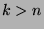 ;
;
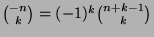 , for
, for
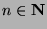 ;
;
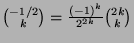 ,
,
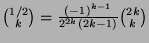 .
.