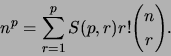Next: About this document ...
Up: prob3
Previous: prob3
- In how many ways can 6 identical balls be coloured
using three colours? What if the balls are distinguishable
(e.g. of different sizes)?
How many of the colourings contain balls of all
three colours, when the balls are
(a) identical, (b) distinguishable?
- How many nonnegative integer triples
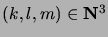 are contained in the plane
are contained in the plane
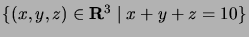 ?
?
- How many different game situations (configurations) are
possible after two plys (move pairs) in a game of tic-tac-toe
on a 3-by-3 board? The board is thought to have
a fixed orientation, so that the ``equivalence'' of
situations under reflections or rotations of the board
need not be considered.
- How many partitions (equivalence relations) are possible
on the set
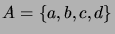 ? Enumerate them.
? Enumerate them.
- [Finnish content.]
- How many anagrams can one obtain from the word TIIVITAAVI?
(Two words are anagrams, if they contain the same
letters in a different order. In the present problem the
anagrams do not need to conform to any phonetic rules.)
- In how many ways can the lecturer (PO) and the four
Teletubbies (Finnish names: Tiivi-Taavi, Hipsu, Laa-Laa,
Pai) be grouped into four nonempty groups.
- The DNA nucleotide sequences that act as the carrier of biological
hereditary information can be viewed as words over the four-letter
alphabet
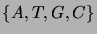 , where the letters correspond to the
nucleotide bases adenine, thymine, guamine, and cytosine.
How many different nucleotide sequences of length 6 are possible?
How many of these contain at least one instance of each base?
How many are such that no base occurs in two adjacent positions?
, where the letters correspond to the
nucleotide bases adenine, thymine, guamine, and cytosine.
How many different nucleotide sequences of length 6 are possible?
How many of these contain at least one instance of each base?
How many are such that no base occurs in two adjacent positions?
- Establish the correctness of the following formula for representing
the integral powers of a number
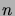 in terms of binomial coefficients:
in terms of binomial coefficients:
(Hint: Consider different ways of selecting a sequence
of length 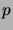 from a basis set of
from a basis set of 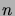 elements.)
Represent the cube
elements.)
Represent the cube 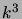 as a sum of the binomial coefficients
as a sum of the binomial coefficients
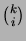 ,
,
 . Prove, using this representation
and the summation formula from problem 4(c) in the previous problem set,
the summation formula for integral cubes:
. Prove, using this representation
and the summation formula from problem 4(c) in the previous problem set,
the summation formula for integral cubes:



Next: About this document ...
Up: prob3
Previous: prob3
Pekka Orponen
2000-10-05