


Next: About this document ...
Up: prob2
Previous: prob2
- Prove the following claims:
- All subsets of the set of natural numbers
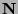 are either finite or countably infinite.
are either finite or countably infinite.
- The cartesian product
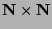 is
countably infinite. (Hint: Think of the pairs
is
countably infinite. (Hint: Think of the pairs
 as laid down
in a two-dimensional table. Enumerate the elements of the table
along diagonals that go in the lower left to upper right direction.)
Note: It follows easily from this result that also
the set of rational numbers
as laid down
in a two-dimensional table. Enumerate the elements of the table
along diagonals that go in the lower left to upper right direction.)
Note: It follows easily from this result that also
the set of rational numbers 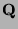 is countably
infinite.
is countably
infinite.
- Prove that in any group of
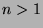 people, there are
at least two persons
who have exactly equally many acquaintances in the group.
A person is not counted among his/her own acquaintances,
and we assume that the acquaintedness relation is symmetric,
so that if
people, there are
at least two persons
who have exactly equally many acquaintances in the group.
A person is not counted among his/her own acquaintances,
and we assume that the acquaintedness relation is symmetric,
so that if 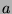 is acuainted with
is acuainted with 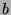 , then also
, then also
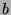 is acquainted with
is acquainted with 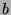 . (Hint: Apply the
pigeonhole principle.)
. (Hint: Apply the
pigeonhole principle.)
- A pack of cards contains 52 cards that are divided into four
``suites'' (hearts, diamonds, clubs, spades). The cards belonging
to each suite are numbered 1,...,13.
- How many different five-card ``poker hands'' (five-card
subsets) are there?
- In how many ways is it possible to form a five-card ``flush'',
i.e. a subset of five cards where all the cards are of the
same suite?
- In how many ways is it possible to form a ``full house'',
i.e. a five-card subset consisting of a ``three-of-a-kind''
(three cards of the same numerical value), and a ``pair''
(two cards of the same numerical value)? The same card in
a full house obviously cannot belong both to the pair and
the three-of-a-kind combination.
- Prove the following properties of the binomial coefficients:
-
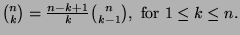 Deduce from this fact that the binomial coefficients
are increasing with respect to the index
Deduce from this fact that the binomial coefficients
are increasing with respect to the index 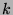 (
(
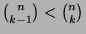 ), when
), when 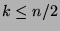 ,
and decreasing
(
,
and decreasing
(
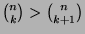 ), when
), when 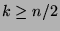 .
.
- Verify Pascal's formula
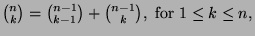 by a direct calculation based on the defining
formula for the binomial coefficients.
by a direct calculation based on the defining
formula for the binomial coefficients.
-
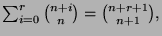 by induction on
by induction on 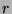 . Which familiar formula do you
obtain from this identity in the case
. Which familiar formula do you
obtain from this identity in the case  ?
Can you come up with a combinatorial argument for
proving the identity?
?
Can you come up with a combinatorial argument for
proving the identity?
- Estimate the size of the ``middlemost'' binomial coefficient
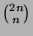 , by approximating the factorial function with
Stirling's formula:
, by approximating the factorial function with
Stirling's formula:
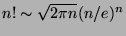 .
.
- Natural numbers
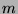 ja
ja 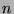 are relatively prime,
if they have no common factors,
i.e. if their greatest common denominator is
are relatively prime,
if they have no common factors,
i.e. if their greatest common denominator is 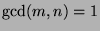 .
The value of Euler's totient function
.
The value of Euler's totient function 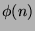 indicates
the number of natural numbers less than
indicates
the number of natural numbers less than 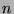 that are relatively
prime to
that are relatively
prime to 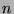 , i.e.
, i.e.
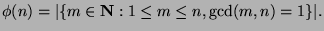 (Thus, for instance,
(Thus, for instance, 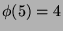 ,
, 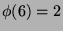 .)
Show, using the inclusion-exclusion principle, that if
the different prime factors of number
.)
Show, using the inclusion-exclusion principle, that if
the different prime factors of number 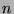 are
are
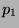 ,
, 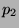 ,...,
,..., 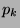 , then
, then



Next: About this document ...
Up: prob2
Previous: prob2
Pekka Orponen
2000-10-05
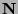 are either finite or countably infinite.
are either finite or countably infinite.
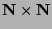 is
countably infinite. (Hint: Think of the pairs
is
countably infinite. (Hint: Think of the pairs
 as laid down
in a two-dimensional table. Enumerate the elements of the table
along diagonals that go in the lower left to upper right direction.)
Note: It follows easily from this result that also
the set of rational numbers
as laid down
in a two-dimensional table. Enumerate the elements of the table
along diagonals that go in the lower left to upper right direction.)
Note: It follows easily from this result that also
the set of rational numbers 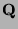 is countably
infinite.
is countably
infinite.
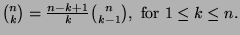 Deduce from this fact that the binomial coefficients
are increasing with respect to the index
Deduce from this fact that the binomial coefficients
are increasing with respect to the index 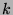 (
(
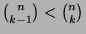 ), when
), when 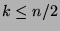 ,
and decreasing
(
,
and decreasing
(
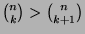 ), when
), when 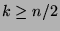 .
.
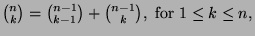 by a direct calculation based on the defining
formula for the binomial coefficients.
by a direct calculation based on the defining
formula for the binomial coefficients.
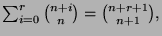 by induction on
by induction on 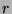 . Which familiar formula do you
obtain from this identity in the case
. Which familiar formula do you
obtain from this identity in the case  ?
Can you come up with a combinatorial argument for
proving the identity?
?
Can you come up with a combinatorial argument for
proving the identity?