Next: About this document ...
Up: me_001129
Previous: me_001129
- Give examples of graphs that contain:
- neither an Eulerian tour (circuit) nor a Hamiltonian cycle;
- an Eulerian tour but no Hamiltonian cycle;
- a Hamiltonian cycle but no Eulerian tour;
- both an Eulerian tour and a Hamiltonian cycle.
- Given a graph
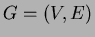 , define the
average degree of its vertices as
, define the
average degree of its vertices as
Prove that for all planar graphs 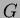 it is the case that
it is the case that
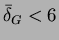 , and that for trees
, and that for trees 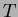 the average
degree approaches the limit value
the average
degree approaches the limit value
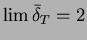 ,
as the number of vertices grows.
,
as the number of vertices grows.
- A hypercube graph
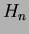 has as vertices all the
has as vertices all the 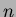 -bit
binary sequences
-bit
binary sequences
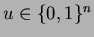 , and vertices
, and vertices 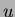 and
and 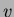 are
connected by an edge if and only if the corresponding binary
sequences differ in exactly one position.
Determine the chromatic number
are
connected by an edge if and only if the corresponding binary
sequences differ in exactly one position.
Determine the chromatic number 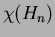 for each
for each 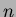 .
(Justify your answer.)
.
(Justify your answer.)
- Design some six-bit, single-error correcting linear code
with 8 codewords. Write down the parity-check matrix
and the set of codewords of your code. Show how you
would use the given parity-check matrix to correct
some word containing a single-bit error.
Grading: Problems 1 and 2 each 8 points, Problems
3 and 4 each 7 points, total 30 points.



Next: About this document ...
Up: me_001129
Previous: me_001129
Pekka Orponen
2000-12-09