


Next: About this document ...
Up: fe_001115
Previous: fe_001115
- Let
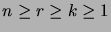 be integers.
Prove the following binomial coefficient identities:
be integers.
Prove the following binomial coefficient identities:
Give also a combinatorial interpretation for the second identity.
- Find the Prüfer codes (as used, e.g., in the proof of Cayley's
theorem) of the following trees:
Determine the 8-vertex tree corresponding to Prüfer code (2,7,1,8,2,8).
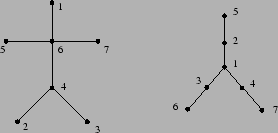
- Prove that every tree
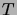 with at least two vertices
has chromatic number
with at least two vertices
has chromatic number 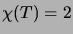 .
.
- Prove that if a tree contains a vertex of degree
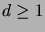 , then it also contains at least
, then it also contains at least 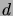 leaves.
leaves.
- Consider a graph whose vertices are
all the two-element subsets of the four-element
basis set
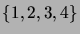 , and there is an edge
between vertices
, and there is an edge
between vertices 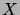 and
and 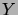 ,
, 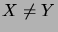 ,
if and only if
,
if and only if
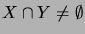 .
Draw a picture of this graph, and prove that it
is planar.
.
Draw a picture of this graph, and prove that it
is planar.
- Prove that the corresponding graph formed out of the
two-element subsets of the five-element basis set
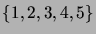 is not planar.
is not planar.
- A tricky situation has developed in the counting of
votes in the presidential election of the Republic of A:
a total of 370 votes given to Donald Duck (who was not
a candidate in the election) should be divided among
the presidential candidates B, G, and N, so that
candidate B gets at least 200 votes, candidate G
gets between 100 and 199 votes, and candidate N gets
at most 10 votes. In how many ways can the duck-votes
be partitioned among the candidates in the desired
manner?
- Consider the set of strings over the four-letter
alphabet
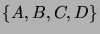 . Denote by
. Denote by 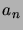 the number
of
the number
of 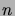 -letter strings that contain an odd number of
the letter
-letter strings that contain an odd number of
the letter 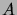 .
(Thus
.
(Thus 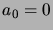 ,
, 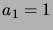 ,
, 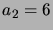 etc.)
Prove that the numbers
etc.)
Prove that the numbers 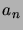 are related by the
recurrence equation
are related by the
recurrence equation
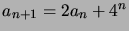 , and
use this recurrence to find a closed-form expression
for the numbers
, and
use this recurrence to find a closed-form expression
for the numbers 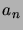 .
(Hint: Partition the
.
(Hint: Partition the 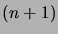 -letter strings
according to whether they begin with
-letter strings
according to whether they begin with 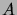 or some
other letter.)
or some
other letter.)
Grading: Each problem 12 points, total 60 points.



Next: About this document ...
Up: fe_001115
Previous: fe_001115
Pekka Orponen
2000-11-15
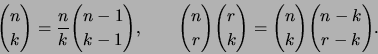
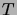 with at least two vertices
has chromatic number
with at least two vertices
has chromatic number 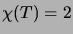 .
.
 , then it also contains at least
, then it also contains at least 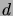 leaves.
leaves.
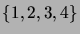 , and there is an edge
between vertices
, and there is an edge
between vertices 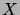 and
and 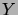 ,
, 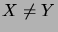 ,
if and only if
,
if and only if
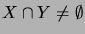 .
Draw a picture of this graph, and prove that it
is planar.
.
Draw a picture of this graph, and prove that it
is planar.
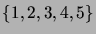 is not planar.
is not planar.