


Next: About this document ...
Up: me_001025
Previous: me_001025
- Let
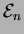 denote the family of all possible
partitions of the set
denote the family of all possible
partitions of the set
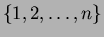 .
Define a partial order
.
Define a partial order 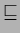 on
on 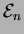 as follows:
as follows:
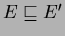 , if partition
, if partition 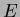 is finer than
partition
is finer than
partition 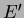 ,
i.e. each class of
,
i.e. each class of 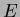 is contained in some class of
is contained in some class of 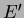 .
For instance, in
.
For instance, in 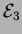 it is true that
it is true that
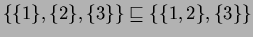 , but
e.g. the partitions
, but
e.g. the partitions
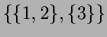 and
and
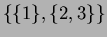 are incomparable.
are incomparable.
- Draw the Hasse diagrams of the partial orders
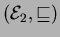 and
and
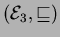 .
How many elements do the sets
.
How many elements do the sets 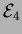 and
and 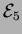 have?
have?
- Describe in general terms the partial order
(
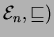 . What are its least and greatest
elements? How many elements does it have altogether?
What are the immediate successors of a given partition
. What are its least and greatest
elements? How many elements does it have altogether?
What are the immediate successors of a given partition
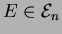 ? How many are there?
? How many are there?
- Consider the family of subsets of an
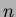 -element set
-element set 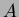 .
How many ways are there to select a pair of sets
.
How many ways are there to select a pair of sets 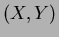 ,
,
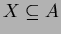 ,
, 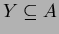 , so that
, so that 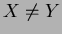 ?
How about if one requires in addition that
?
How about if one requires in addition that 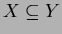 ?
?
- Six married couples organize a dance party. In how many ways
can they be arranged into dancing pairs, when it is required
that nobody dances with their own spouse?
(Hint: Inclusion-exclusion.)
- Small-time stock market investor F. U. Ture manages
his portfolio according to the following scheme:
in the beginning of each week he buys new shares for
an amount of money equal to the value of his portfolio
two weeks earlier, and sells shares for an amount
corresponding to the value of his portfolio three
weeks earlier. (Any other possible changes in the
values of the shares are ignored here.) Find out how
the value of F. U. Ture's portfolio evolves, when he
starts investing in the beginning of Week 0 with
an initial capital of 1 Euro.
Grading: Problems 1 and 4 each 8 points, Problems
2 and 3 each 7 points, total 30 points.



Next: About this document ...
Up: me_001025
Previous: me_001025
Pekka Orponen
2000-10-25
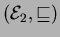 and
and
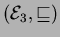 .
How many elements do the sets
.
How many elements do the sets 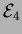 and
and 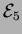 have?
have?
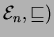 . What are its least and greatest
elements? How many elements does it have altogether?
What are the immediate successors of a given partition
. What are its least and greatest
elements? How many elements does it have altogether?
What are the immediate successors of a given partition
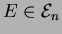 ? How many are there?
? How many are there?