Next: Tästä dokumentista ...
Up: harj3
Previous: harj3
- Monellako tavalla 6 identtistä palloa voidaan
värittää kolmella värillä? Entä jos pallot ovat
toisistaan erottuvia (esim. erikokoisia)?
Moniko värityksistä sisältää kaikkien kolmen
värisiä palloja, kun pallot ovat (a) identtisiä
(b) erottuvia?
- Monenko ei-negatiivisten kokonaislukujen muodostaman kolmikon
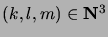 kautta kulkee avaruuden
kautta kulkee avaruuden 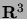 taso
taso
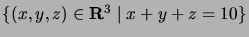 ?
?
- Montako erilaista mahdollista pelitilannetta on
3
 3-jätkänshakissa (ristinollassa) kahden
siirtoparin jälkeen? (Tilanteiden samaistamista
pelilaudan kiertojen ja peilausten avulla ei tarvitse
tarkastella.)
3-jätkänshakissa (ristinollassa) kahden
siirtoparin jälkeen? (Tilanteiden samaistamista
pelilaudan kiertojen ja peilausten avulla ei tarvitse
tarkastella.)
- Montako ositusta (ekvivalenssirelaatiota) voidaan määritellä
joukossa
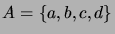 ? Luettele ne.
? Luettele ne.
- Kuinka monta anagrammia voidaan muodostaa sanasta TIIVITAAVI?
(Kaksi sanaa ovat anagrammeja, jos niissä on samat
kirjaimet eri järjestyksessä. Tässä tehtävässä anagrammien
ei tarvitse olla suomenkielen äänneopin mukaisia.)
- Kuinka monella tavalla luennoija (PO) ja neljä teletappia
(Tiivi-Taavi, Hipsu, Laa-Laa ja Pai) voidaan ryhmitellä kolmeen
ryhmään niin, että mikään ryhmistä ei ole tyhjä?
- Biologisen perimäinformaation kantajina toimivia nukleotidijonoja
voidaan tarkastella nelikirjaimisen aakkoston
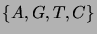 sanoina, joiden kirjaimet vastaavat nukleotidiemästen adeniini,
tymiini, guaniini ja sytosiini esiintymiä. Montako erilaista 6 merkin
mittaista nukleotidijonoa on olemassa? Moniko näistä sisältää
ainakin yhden kappaleen kutakin nukleotidiemästä? Entä montako
on sellaista, joissa ei mikään nukleotidiemäs esiinny kahdessa
vierekkäisessä positiossa?
sanoina, joiden kirjaimet vastaavat nukleotidiemästen adeniini,
tymiini, guaniini ja sytosiini esiintymiä. Montako erilaista 6 merkin
mittaista nukleotidijonoa on olemassa? Moniko näistä sisältää
ainakin yhden kappaleen kutakin nukleotidiemästä? Entä montako
on sellaista, joissa ei mikään nukleotidiemäs esiinny kahdessa
vierekkäisessä positiossa?
- Todista oikeaksi kokonaislukujen potenssien binomikerroinesityksiä
koskeva muunnoskaava:
(Vihje: Tarkastele 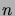 -alkioisesta perusjoukosta muodostettujen
-alkioisesta perusjoukosta muodostettujen
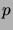 -jonojen erilaisia valintatapoja.) Lausu potenssi
-jonojen erilaisia valintatapoja.) Lausu potenssi 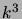 binomikertoimien
binomikertoimien
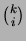 ,
,
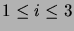 , summana. Osoita
em. esitystä ja harjoitusten 2 tehtävän 4(c) summaussääntöä
käyttäen todeksi summakaava
, summana. Osoita
em. esitystä ja harjoitusten 2 tehtävän 4(c) summaussääntöä
käyttäen todeksi summakaava



Next: Tästä dokumentista ...
Up: harj3
Previous: harj3
Pekka Orponen
2000-10-05