The adaptations rules in (28) and (30) assume other parameters to be constant. The weights, sources and biases are updated all at once, however, because it would not be computationally efficient to update only one at a time. The assumption of independence is not necessarily valid, particularly for the posterior means of the variables, which may give rise to instabilities. Several variables can have a similar effect on outputs and when they are all updated to the values which would be optimal given that the others stay constant, the combined effect is too large.
This type of instability can be detected by monitoring the directions
of updates of individual parameters. When the problem of correlated
effects occurs, consecutive updated values start oscillating. A
standard way to dampen these oscillations in fixed point algorithms is
to introduce a learning parameter ![]() for each parameter and
update it according to the following rule:
for each parameter and
update it according to the following rule:
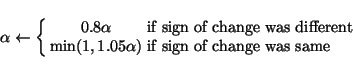 |
(30) |
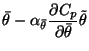 |
(31) | ||
![$\displaystyle \frac{1}{\left[ 2 \frac{\partial
C_p}{\partial \tilde{\theta}} \right]^{\alpha_{\tilde{\theta}}}}
\tilde{\theta}^{1 - \alpha_{\tilde{\theta}}}$](img84.gif) |
(32) |