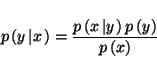Approximations of posterior pdf

As we have shown earlier, the posterior distribution is a synonym for our available knowledge of a system after we have made a set of observations. In order to use this knowledge we will typically be required to marginalise the posterior or to evaluate expectations of functions under the posterior distribution. In many problems it is intractable to perform the necessary integrals.

If we look again at Bayes equation we have

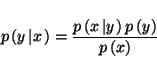$$p\left(y\left\vert x\right.\right) = \frac{p\left(x\left\vert y\right.\right)p\left(y\right)}{p\left(x\right)}$$ (3)

It is easy to compute one point in the joint density $p\left(x,y\right)$ (the numerator of the posterior distribution) but in general evaluating the denominator, $p\left(x\right)$, is difficult. Similarly marginalising the posterior distribution is difficult.

Therefore it is necessary to approximate the posterior density by a more tractable form for which it is possible to perform any necessary integrals. We cannot take a point estimate (such as the MAP estimate) because this leads to overfitting as shown earlier. This is because the MAP estimate does not guarantee a high probability mass in the peak of the posterior distribution and so the posterior distribution may be sharp around the MAP estimate. We would like to approximate the probability mass of the posterior.

There are in general two types of approximation that retain the probability mass of the true posterior distribution. The first type is the stochastic approximation and the second type is the parametric approximation. In a stochastic approximation (such as Markov-chain Monte Carlo method) the aim is to perform the integrations by drawing samples from the true posterior distribution, [3]. The average of any function is then found by finding the average value of the function given all of the samples from the posterior.

In a parametric approximation (such as Laplace approximation, [6]) the posterior distribution is approximated by an alternative function (such as a Gaussian) such that it is much simpler to perform any necessary approximations.

The problem with the stochastic methods is that when performing a stochastic approximation it is necessary to wait until the sampler has sampled from all of the mass of the posterior distribution. Therefore testing for convergence can be a problem. The problem with the parametric approach is that the integrals that are being performed are not exactly the same as those that would be performed when the true posterior is used. Therefore while the stochastic approximation has to give the correct answer (eventually) the parametric approxmation will give an approximate answer soon (it is the `quick and dirty' method).

Model selection can be seen as a special form of approximating the posterior distribution. The posterior distribution could contain many peaks, but when there is lots of data, most of the probability mass is typically contained in a few peaks of the posterior distribution. Model selection means using only the most massive peaks and discarding the remaining models.