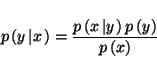 |
(1) |
When we say we are making a model of a system, we are setting up a tool which can be used to make inferences, predictions and decisions. Each model can be seen as a hypothesis, or explanation, which makes assertions about the quantities which are directly observable and which can only be inferred from their effect on observable quantities.
In the Bayesian framework, knowledge is contained in the conditional probability distributions of the models. We can use Bayes' theorem to evaluate the conditional probability distributions for the unknown parameters, y, given the set of observed quantities, x, using
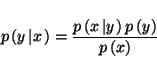 |
(1) |
There is no clear cut difference between the prior and posterior distributions, since after a set of observations the posterior distribution becomes the prior for another set of observations.
In order to make inferences based on our knowledge of the system, we need to marginalise our posterior distribution with respect to the unknown parameters of the model. For instance in order to obtain the average values of the unknown parameters we would need to perform the expectation
 |
(2) |
Alternatively we may be trying to use our model of the system to make decisions about which action to take. In this case we would like to choose the action which maximises some utility function. In this case the expected utility is found by marginalising the utility function over the posterior density of the models. An example would be hypothesis testing where we have a number of explanations for the cause of a set of observed data. By having a different model for each hypothesis, we could choose the model that maximises the expected utility.
In this chapter we shall motivate the idea of considering the posterior distribution to be the result of any experiment instead of just considering a point in the model space. Section 3 will discuss different methods of approximating the posterior when it is intractable to make inferences based on the true posterior. Section 4 will introduce the idea of using Ensemble Learning to approximate the true posterior by a simpler separable distribution. Section 5 will discuss the construction of probabilistic models, both in supervised and unsupervised learning. Section 6 will give examples of using ensemble learning in both a fixed form and free form approximation.