Rabiner [48] lists three basic problems for HMMs:
Problem 1 is not a learning problem but rather one needed in
evaluating the model. Its difficulty comes from the fact that one
needs to calculate the sum over all the possible state sequences.
This can be diverted by calculating the probabilities recursively with
respect to the length of the observation sequence. This operation
forms one half of the forward-backward algorithm and it is
very typical for HMM calculations. The algorithm uses an auxiliary
variable
![]() which is defined as
which is defined as
The algorithm to evaluate
![]() proceeds as follows:
proceeds as follows:
![$\displaystyle \alpha_j(t+1) = \left[ \sum_{i=1}^N \alpha_i(t) a_{ij} \right] b_j(x(t+1))$](img153.gif) |
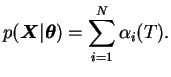 |
The solution of Problem 2 is much more difficult. Rabiner uses classical statistics and interprets it as a maximum likelihood estimation problem for the state sequence, the solution of which is given by the Viterbi algorithm. A Bayesian solution to the problem can be found with a simple modification of the solution of the next problem which essentially uses the posterior of the hidden states.
Rabiner's statement of Problem 3 is more precise than ours and asks
for the maximum likelihood solution optimising
![]() with
respect to
with
respect to
![]() . This problem is solved by the Baum-Welch
algorithm which is an application of the EM algorithm to the problem.
. This problem is solved by the Baum-Welch
algorithm which is an application of the EM algorithm to the problem.
The Baum-Welch algorithm uses the complete forward-backward
procedure with a backward pass to compute
![]() . This can be done very much like the forward pass:
. This can be done very much like the forward pass:
![$\displaystyle \beta_i(t) = b_i(x(t)) \left[ \sum_{j=1}^N a_{ij} \beta_j(t+1) \right].$](img157.gif) |
The M-step of Baum-Welch algorithm can be expressed in terms of
![]() , the posterior probability that there was a transition
between state
, the posterior probability that there was a transition
between state ![]() and state
and state ![]() at time step
at time step ![]() given
given
![]() and
and
![]() . This probability can be easily calculated with forward and
backward variables
. This probability can be easily calculated with forward and
backward variables ![]() and
and ![]() :
: